【時系列解析】1/fゆらぎを積分するとパワースペクトルの指数が2だけ変化（解析的導出）

今回は，「 $1/f^{\beta}$ ゆらぎを積分すると， $1/f^{\beta+2}$ ゆらぎになる」ことの説明です．

つまり，時系列 $\left\{ x[i] \right\}_{i=0}^{N-1}$ のパワースペクトル $S_x(f)$ が，低周波数側で

　 $\displaystyle S_x(f) \propto \frac{1}{f^{\beta}}$

に従うとき， $\left\{ x[i] \right\}_{i=0}^{N-1}$ を積分した時系列

　 $y[i] = \displaystyle \sum_{k=0}^{i-1} x[k$ ]　　( $i=1, 2, \cdots, N$ )

のパワースペクトル $S_y(f)$ が，低周波数側で

　 $S_y(f) \propto \displaystyle \frac{1}{f^{\beta+2}}$

になることの説明です（下図参照）．逆に，差分をとると $\displaystyle \frac{1}{f^{\beta-2}}$ になります．

これは， $\frac{1}{f^{\beta}}$ ゆらぎを生成するためには，積分や差分の拡張して（2ずつの傾き変化でなく），非整数積分や非整数差分を導入すればいいな（自由に傾きをかえられる），というアイデアにつながる重要な事実です．

既に知っている1次自己回帰過程で考察

1次自己回帰過程

　 $y [n ]=a y [n-1] + w [n ]$

で， $a=1$ として， $x [n] = w [n+1 ]$ とすれば，

　 $y[i] = \displaystyle \sum_{k=0}^{i-1} x[k$ ] 　　( $i=1, 2, \cdots, N$ )

の形になってます．このとき， $\left\{ x[i] \right\}_{i=0}^{N-1}$ は，白色ノイズなので，

　 $\displaystyle S_x(f) \propto \frac{1}{f^{0}} =$ (定数)

です． $y[i]$ のパワースペクトルについては， $a < 1$ で， $a$ が1に近いときは，高周波数側で

　 $\displaystyle S_y (f) \approx \frac{\sigma^2}{ 4 \pi^2 a f^2} \propto \frac{1}{f^{2}}$

と近似できます（以前の記事で説明しました）．
chaos-kiyono.hatenablog.com

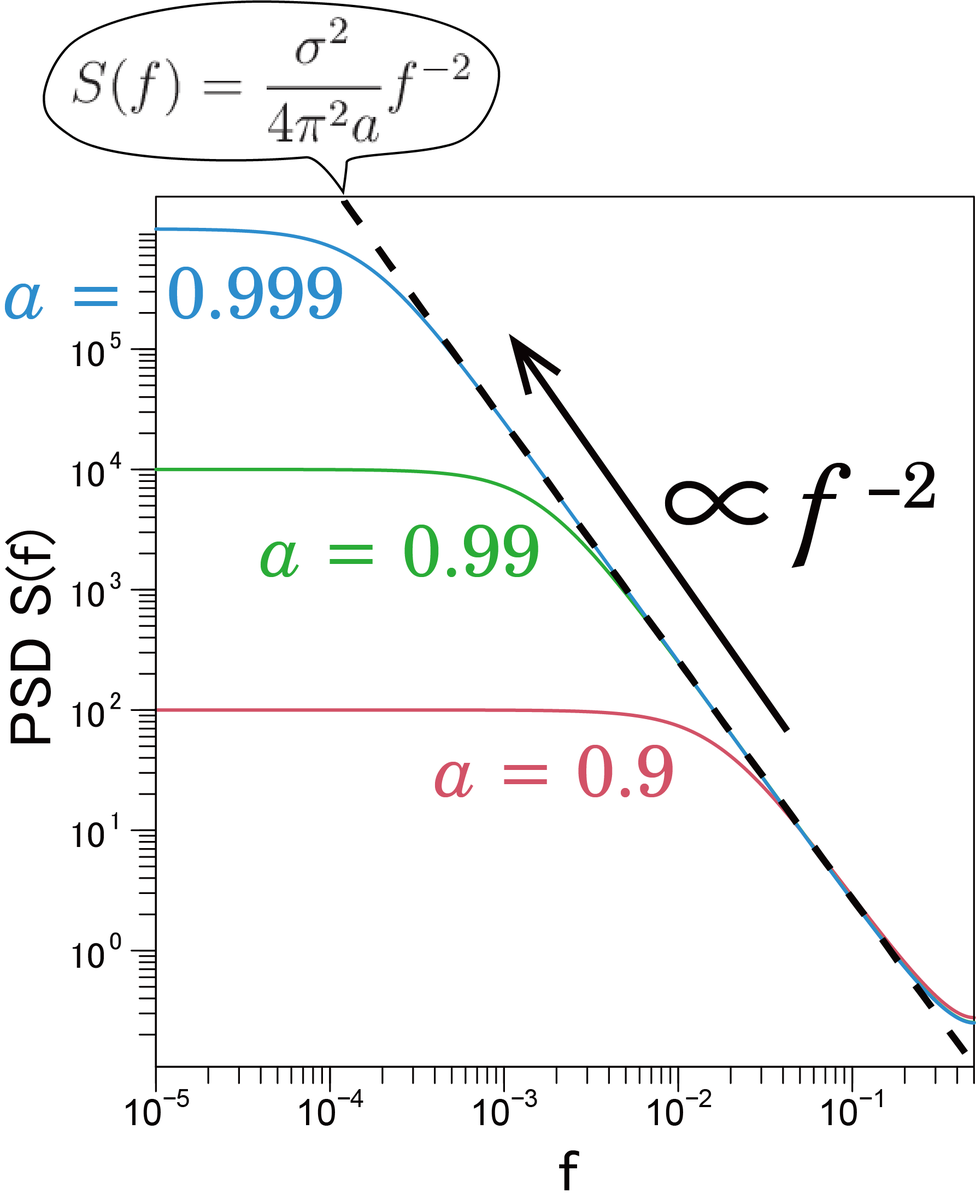
ですので，上の図のように， $a \to 1$ とすれば，これがどんどん低周波数側に広がるので，最終的に，低周波数側でも，

　 $S_y(f) \propto \displaystyle \frac{1}{f^{2}} = \frac{1}{f^{0+2}}$

となることが期待できます．ですので， $f^0$ から $f^{-2}$ に変化することが分かります．

数学者のように細かいことを言うと， $\{ y[i] \}$ のパワースペクトルは存在しません．なぜなら， $n \to \infty$ で時系列の分散が発散するので，パワースペクトル密度の全面積も発散するからです．

ということで，有限長の時系列を考える必要があります．

ここでの問題設定は，有限長の確率過程のサンプル時系列を積分して，そのパワースペクトルの推定値を計算するとどうなるか？です．

有限長時系列を積分したときのパワースペクトルの変化（解析的にやる）

　 $\left\{ x[i] \right\}_{i=0}^{N-1}$ のフーリエ変換を $X(f_k)$ とします．ここで， $f_k = k/N$ です．Nが奇数のときのみ正しい説明をします（偶数のときはf=1/2の扱いのみ違います）．

フーリエ変換の結果 $X(f_k)$ を使えば，

　 $\displaystyle x[i] = \sum_{k=-(N-1)/2}^{k=(N-1)/2} A_k \cos (2 \pi f_k i + \theta_k)$

と表せます．ここで， $A_k = \frac{|X(f_k)|}{N}$ ， $\theta_k = {\rm arg} X(f_k)$ です．

$y[i] = \displaystyle \sum_{j=0}^{i-1} x[j]$ の計算では，

　 $\displaystyle y[i] = \sum_{j=0}^{i-1} \sum_{k=-(N-1)/2}^{k=(N-1)/2} A_k \cos (2 \pi f_k j + \theta_k) = \sum_{k=-(N-1)/2}^{k=(N-1)/2} \left(\sum_{j=0}^{i-1} A_k \cos (2 \pi f_k j + \theta_k) \right)$

となるので，周波数成分ごとに和をとることにします．

$\cos$ の和の公式

　 $\displaystyle \sum_{k=0}^{i-1} \cos\left( a k \right) = \frac{\sin \frac{a}{2}i}{\sin \frac{a}{2}} \cos \frac{a(i-1)}{2}$

を使えば，

　 $\displaystyle \sum_{j=0}^{i-1} A_k \cos (2 \pi f_k j + \theta_k) =\frac{A_k}{2 \sin (\pi f_k)} \left\{\sin(2 \pi f_k i - \pi f_k + \theta_k ) +\sin (\pi f_k - \theta)\right\}$

となります．この中で定数項は，パワースペクトルの傾きの議論には寄与しないので，

　 $\displaystyle \sum_{k=0}^{i-1} A_k \cos (2 \pi f_k i + \theta_k) \propto \frac{A_k}{2 \sin (\pi f_k)} \sin(2 \pi f_k i - \pi f_k + \theta_k )$

を考えれば十分です．もっといえば，各周波数成分の振幅が，積分の前後で，

　 $A_k$

から，

　 $\displaystyle \frac{A_k}{2 \sin (\pi f_k)}$

になる結果を使うだけで，結論が導けます．周波数fが小さい領域を考えるので，ローラン展開（複素関数論ででてきます）をつかって，主要項のみ残せば（分母にsin x = xの近似でも構いません），

　 $\displaystyle \frac{A_k}{2 \sin (\pi f_k)} \approx \frac{A_k}{2 \pi f_k}$

となります．

ということで， $S_x(f_k) \propto f_k^{-\beta} \propto A_k^2$ なので，

　 $S_y(f_k) \propto \left( \frac{A_k}{2 \pi f_k} \right) ^2 = \frac{A_k^2}{\left(2 \pi f_k\right) ^2}= \frac{f_k^{-\beta}}{\left(2 \pi f_k\right) ^2} \propto f_k^{-\beta-2}$

が導けました．パワースペクトルが存在するとかの話ではなく，有限長時系列でパワースペクトルの推定量の計算をすれば，これが成り立つということです．

ケィオスの時系列解析メモランダム

時系列解析，生体情報学，数学・物理などの解説です．

【時系列解析】1/fゆらぎを積分するとパワースペクトルの指数が2だけ変化（解析的導出）

既に知っている1次自己回帰過程で考察

有限長時系列を積分したときのパワースペクトルの変化（解析的にやる）