【基礎工学のための複素関数論】留数定理 - ケィオスの時系列解析メモランダム

今回は留数定理です．留数定理を知っておいてほしい理由は，自己回帰過程の分解の計算に使うからです．留数定理では，下図のように周回積分する単一閉曲線 $C$ の内側に，特異点と呼ばれるトゲや穴 $z_1$ ， $z_2$ ， $z_3$ が複数ある場合を扱えます．

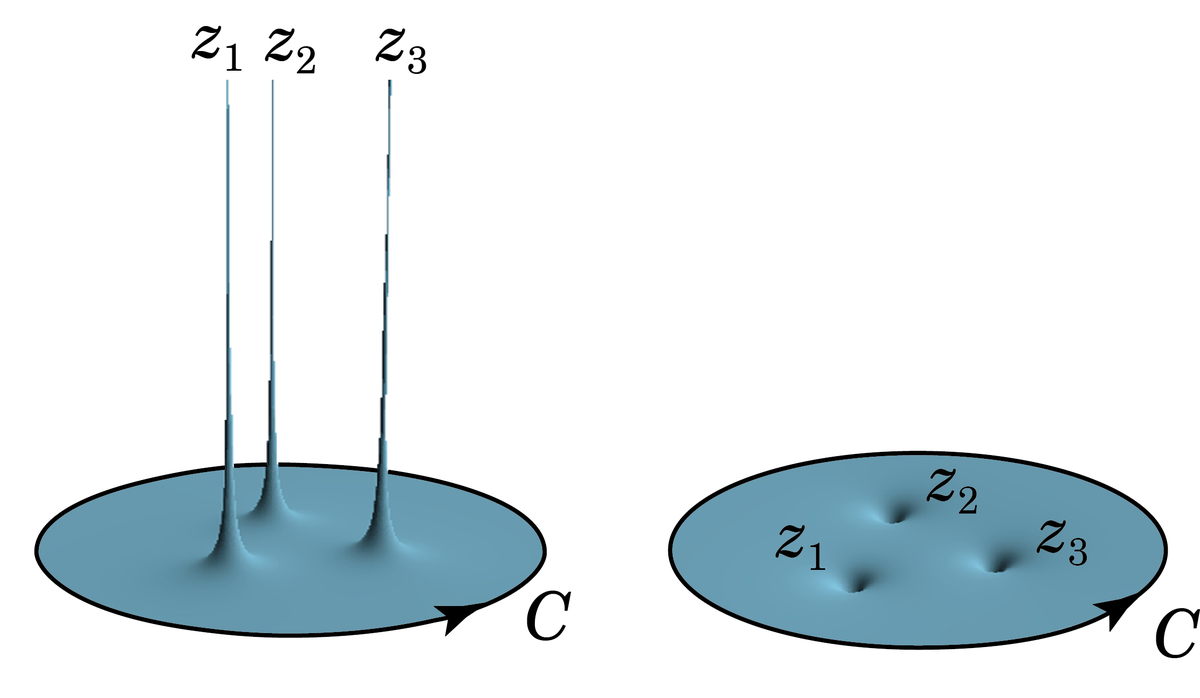
複素平面にある特異点のイメージ (実際は実部と虚部それぞれに値があるので一つの図で表せない)．単一閉曲線 $C$ の内側に，特異点 $z_1$ ， $z_2$ ， $z_3$ がある場合．

基本事項の確認

　前回紹介した複素積分のポイントは，下図のように，周回積分する単一閉曲線 $C$ の内側に，特異点と呼ばれるトゲあるいは穴 $z_0$ が一つあるかどうかです．トゲと穴は，それぞれ，無限とマイナス無限までのびています．私は，下図右の絵のような穴を感じるので，落ちてしまいそうで怖いです (実際はプラスのとき上向きに発散するトゲで，マイナスのとき穴です)．それと，周回積分で回る方向は，反時計回り (内部を左側にするまわり方)です．なぜなら，陸上ではトラック左周りが世界のルールです (複素積分とは関係ありません)．

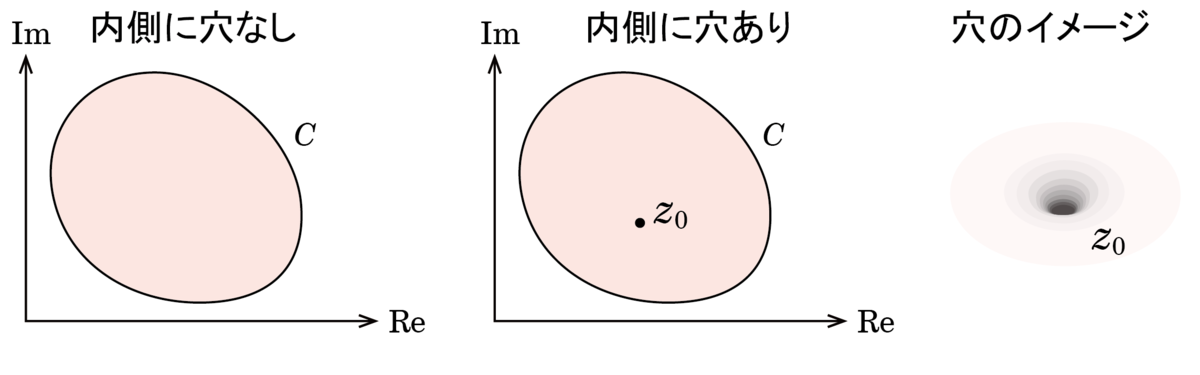
1．周回する内側が全部正則 (穴なし)なら周回積分はゼロ

関数 $f(z)$ は，単一閉曲線 $C$ とその内部を含む領域で正則であるとする (上図左)．このとき，

　 $\displaystyle \oint_C \! f(z) \, dz = 0$

2．周回する内側に穴 (特異点)があれば，その値を分子に代入する感じ

積分経路の中に穴 $z_0$ (分母が0になる特異点)があれば (上図中)，積分は分子の部分に $z_0$ を代入するだけで求まっちゃう：

　 $\displaystyle \oint_C \frac{f(z)}{z-z_0} \, dz = 2 \pi i f(z_0)$

積分経路の中に穴 $z_0$ (特異点)があって，それが $n$ 乗でより深くなっていれば， $(n-1)$ 回微分を繰り返してから， $z_0$ を代入するだけで求まっちゃう：

　 $\displaystyle \oint_C \frac{f(z)}{(z-z_0)^{n}} \, d z = \frac{2 \pi i}{(n-1)!} f^{(n-1)}(z_0)$

留数定理を理解する一歩手前

　下図左のように，単一閉曲線 $C$ の内側に3つの穴があるとします．

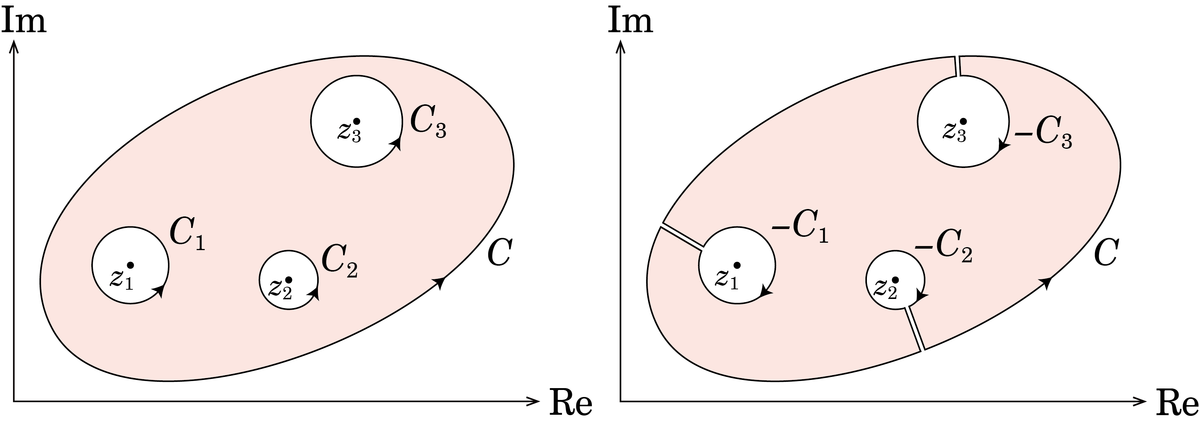
このとき，単一閉曲線 $C$ についての周回積分は，3つの穴のまわりを回る，周回積分に分割できます．

　 $\displaystyle \oint_C f(z) \, d z = \oint_{C_1} f(z) \, d z + \oint_{C_2} f(z) \, d z + \oint_{C_3} f(z) \, d z$

なぜかは，上図の右のような周回積分を考えれば説明できます．切り込みの出入は積分経路が逆になっているので，積分は符号が逆になり，和をとるとゼロになります．ですので，基本事項1 (コーシーの積分定理)を使って，

　 $\begin{eqnarray} \oint_{C-C_1-C_2-C_3} f(z) \, d z &=& 0 \\ \oint_{C} f(z) \, d z -\oint_{C_1} f(z) \, d z - \oint_{C_2} f(z) \, d z - \oint_{C_3} f(z) \, d z &=& 0 \\ \oint_C f(z) \, d z &=& \oint_{C_1} f(z) \, d z + \oint_{C_2} f(z) \, d z + \oint_{C_3} f(z) \, d z \end{eqnarray}$