【確率過程・時系列解析】2次自己回帰過程の自己共分散 (自己相関)関数

2次自己回帰過程の自己共分散 (自己相関)関数を一つの式で表しておきます．差分方程式の形での表現は，この前のセミナーで学生が導いてくれたし，インターネットで検索すればいくらでも出てくると思います．

2次自己回帰過程

　今回，考えるのはこれです．

　 $y[n] = a_1 y[n-1] +a_2 y[n-2] + w[n]$

ここで， $a_1$ ， $a_2$ は実数のパラメタ， $\{w[n]\}$ は平均0，分散 $\sigma^2$ の白色ノイズです．このとき，自己共分散 (自己相関)関数が，次のようになることを導きます．

「 $a_1^2+4 a_2 < 0$ 」の2次自己回帰過程の自己共分散 (自己相関)関数

　 $\begin{eqnarray} C(k) &=& c_0\, r^k \cos \left( \omega k \right) + c_1 r^k \sin \left( \omega k \right) \end{eqnarray}$

ここで，
　 $\begin{eqnarray} c_0 &=& \frac{\sigma^2 (1-a_2)}{(1+a_2)(1-a_1-a_2)(1+a_1-a_2)} \\ c_1 &=& \frac{a_1 \sigma^2}{(1-a_1-a_2)(1+a_1-a_2) \sqrt{-(a_1^2+4 a_2)}} \\ r &=& \sqrt{-a_2} \\ \omega &=& \arctan \frac{\sqrt{-\left(a_1^2+4 a_2 \right)}}{a_1} \end{eqnarray}$

ポイントは，
　
　自己共分散 (自己相関)関数が，指数関数的減衰と三角関数の積になっている

ということです．

（今回，この式を生まれてはじめて導きました．他の仕事がたくさんあるのに，この計算に時間をかけてしまいました．関係者の方すいません.）すごく基本的な式だと思いますが，間違えていると申し訳ないので，この式が載っている本や論文やホームページがあれば教えてください．導出の過程で，正負の吟味や，絶対値を付けるかなど，表現を迷ったところがあるので，間違いがあれば教えてください．

自己共分散 (自己相関)関数の差分方程式表現

　多くの教科書に載っている，2次自己回帰過程の自己共分散 (自己相関)関数 $C(k)$ はこれです．

$\begin{eqnarray} C(0) &=& \frac{\sigma^2 (1-a_2)}{(1+a_2)(1-a_1-a_2)(1+a_1-a_2)} \\ C(1) &=& \frac{a_1}{1-a_2} C(0) \\ C(k) &=& a_1 C(k-1) + a_2 C(k-2) \qquad (C \ge 2) \end{eqnarray}$

導出過程は省略します．検索すれば，丁寧に説明してあるページを見つけられると思います．

　この結果を示されると，「一つの式で書けないの？」と疑問がわきます．

だって，これだと不便な感じがします．例えば，自己共分散 (自己相関)関数 $C(k)$ がどんな形なのか，一見して想像できません．

自己共分散 (自己相関)関数を一つの式で表してみる

　上の差分方程式表現を使って，私が計算した結果を示します (間違っていたらすいません)．漸化式を解くだけなので高校生でも解けるかというと，そんなに簡単ではありません．複素数の極形式や逆三角関数の関係式なんかを使います．

　ということで，2次自己回帰過程の自己共分散 (自己相関)関数 $C(k)$ はこれです．

2次自己回帰過程

　 $y[n] = a_1 y[n-1] +a_2 y[n-2] + w[n]$ ( $\{w[n]\}$ は平均0，分散 $\sigma^2$ )

において， $a_1^2+4 a_2 < 0$ のとき，自己共分散 (自己相関)関数は，

　 $\begin{eqnarray} C(k) &=& \frac{C(1)}{{\rm Im} \, \lambda} r^k \sin \left( \omega k \right) - \frac{C(0)}{{\rm Im}\, \lambda} r^{k+1} \sin \left( \omega (k-1) \right) \\ \\ &=& C(0)\, r^k \cos \left( \omega k \right) + C(0) \frac{a_1 + a_1 a_2}{(1-a_2) \sqrt{-(a_1^2+4 a_2)}} r^k \sin \left( \omega k \right) \end{eqnarray}$

ここで，

　 $\begin{eqnarray} \lambda &=& \frac{a_1 + i \sqrt{-\left(a_1^2+4 a_2 \right)} }{2} \\ {\rm Re} \, \lambda &=& \frac{a_1}{2} \\ {\rm Im} \, \lambda &=& \frac{\sqrt{-\left(a_1^2+4 a_2 \right)} }{2} \\ r &=& \left| \lambda \right| = \sqrt{-a_2} \\ \omega &=& \arctan \frac{{\rm Im} \, \lambda}{{\rm Re} \, \lambda} = \arctan \frac{\sqrt{-\left(a_1^2+4 a_2 \right)}}{a_1} \end{eqnarray}$

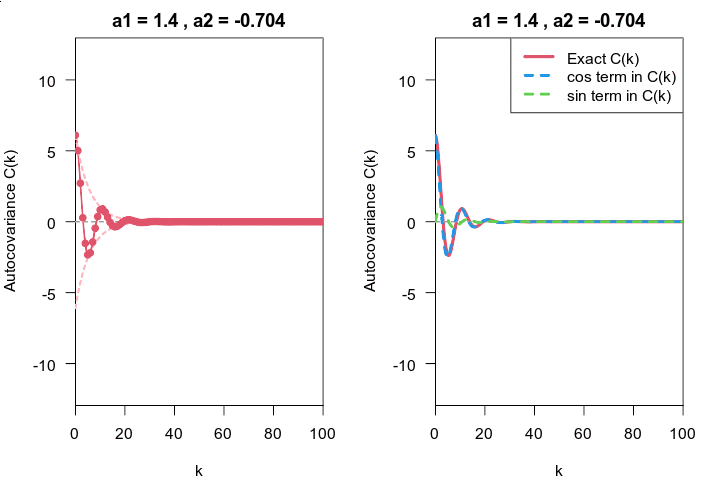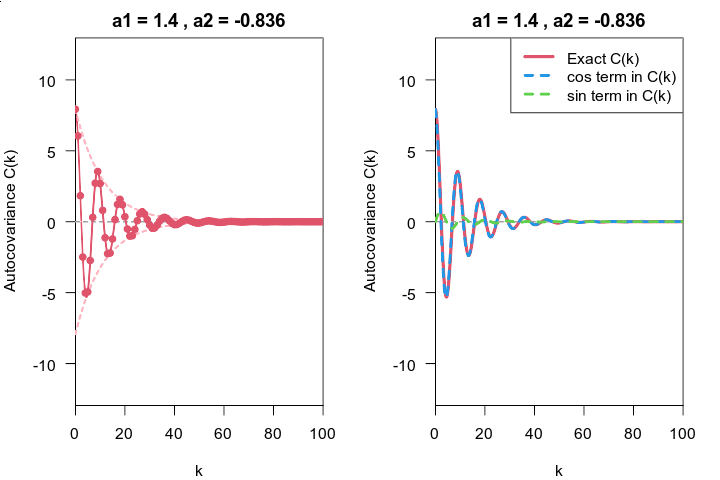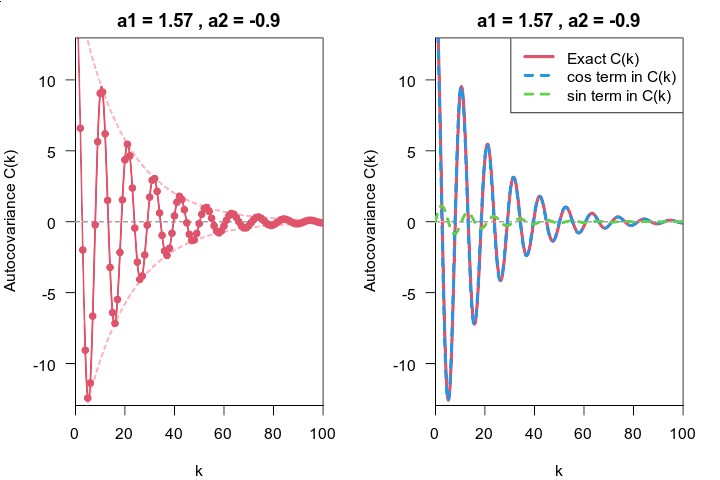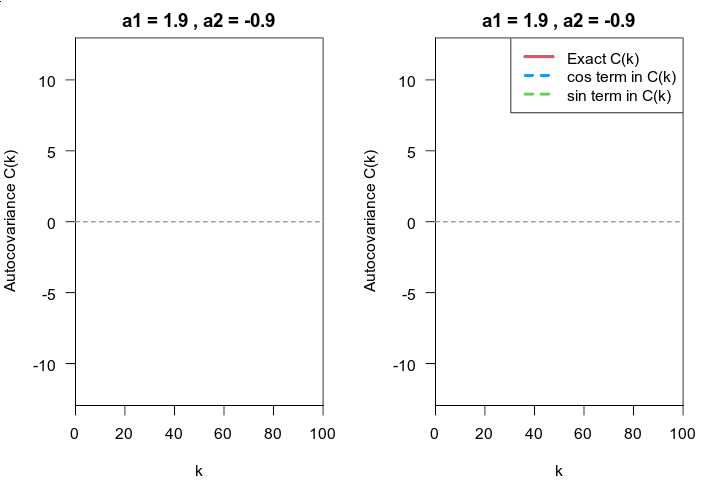
　私は計算能力に自信がないので，解析的に計算してみたら，必ず数値的に検証します．Rで差分方程式を使った自己共分散 (自己相関)関数 $C(k)$ と今回導いたもののグラフを重ねると，以下のようになりました．

解析的に計算した自己共分散 (自己相関)関数．(上) 差分方程式表現．(中) 今回導出した結果．(下) 差分方程式表現と今回導出した結果を重ねたグラフ．

上図のグラフは，一番上が差分方程式表現，その下が今回導出した結果，一番下が，差分方程式表現と今回導出した結果を重ねたグラフです．正しそうです．

　導出には，3項間の漸化式の解き方を使います．私が高校生のころは，ちょっと発展的な参考書に解き方が載っていました．他は，複素数の知識も計算には必要です．

　こんなのテストに出ないし，研究の論文にもならないのに，何でやっているの？と疑問に思うかもしれません．こういった計算を地道にやり，知識と感覚を養っていくことが，新しい結果をみつけて，論文を書くためには必要なのです．少なくとも私のやり方はこれです．時系列の分析に，Rとか，Pythonとかの何かよく分からない関数やパッケージを使って，なんとなくこねくりまわしてみる．そんなやり方をしている研究者もいるかもしれません．それもありだと思いますが，それだと物事を理解したときの喜びは小さいような気がします．

おまけ

　グラフを描くときに使ったRスクリプト.

####################
# パラメタ (parameter)
a1 <- 0.9*sqrt(3)
a2 <- -0.81
# w[n]の標準偏差sig^2
sig2 <- 1
########
# 差分方程式表現した自己共分散関数
m <- 100
acov <- c()
acov[1] <- sig2/((1-a2)^2-a1^2)*(1-a2)/(1+a2)
acov[2] <- a1/(1-a2)*acov[1]
for(i in 3:(m+1)){
 acov[i] <- a1*acov[i-1]+a2*acov[i-2]
}
# グラフを描く
par(mfrow=c(3,1),mar=c(4,4,1,1),cex=1.3)
plot(0:m,acov,"o",pch=16,col=3,lwd=2,xlab="Lag k", ylab="Autocovariance C(k)",las=1)
##############################
# 導出した結果
roots <- polyroot(c(a2,a1,-1))
root <- roots[1]
r <- abs(root)
ImL <- Im(root)
omega <- atan(ImL/Re(root))
# C(0)をC(1)は， 差分方程式表現で計算した結果を使わせてもらいます．
C0 <- acov[1]
C1 <- a1/(1-a2)*acov[1]
##############################
# グラフを描く
curve(C0*r^x*cos(omega*x)+C0*((a1+a1*a2)/((1-a2)*sqrt(-a1^2-4*a2)))*r^x*sin(omega*x),n=1000,col=2,lwd=2,xlim=c(0,m),ylab="Autocovariance C(k)",las=1)
points(0:m,C0*r^(0:m)*cos(omega*(0:m))+C0*((a1+a1*a2)/((1-a2)*sqrt(-a1^2-4*a2)))*r^(0:m)*sin(omega*(0:m)),col=2)
# グラフを重ねて描いてみる
plot(0:m,acov,"o",pch=16,col=3,lwd=2,xlab="Lag k", ylab="Autocovariance C(k)",las=1)
curve(C0*r^x*cos(omega*x)+C0*((a1+a1*a2)/((1-a2)*sqrt(-a1^2-4*a2)))*r^x*sin(omega*x),add=TRUE,n=1000,col=2,lwd=2,lty=2)
points(0:m,C0*r^(0:m)*cos(omega*(0:m))+C0*((a1+a1*a2)/((1-a2)*sqrt(-a1^2-4*a2)))*r^(0:m)*sin(omega*(0:m)),col=2)

ケィオスの時系列解析メモランダム

時系列解析，生体情報学，数学・物理などの解説です．

【確率過程・時系列解析】2次自己回帰過程の自己共分散 (自己相関)関数

2次自己回帰過程

自己共分散 (自己相関)関数の差分方程式表現

自己共分散 (自己相関)関数を一つの式で表してみる

おまけ