【Rで聴覚の不思議】無限音階「シェパード・トーン」の紹介

最近，音の認知について少しずつ勉強しています．今回は「錯聴」と呼ばれる音のイリュージョン (錯覚)の話です．

　有名な錯聴の一つに「シェパード・トーン」(Shepard tone)と呼ばれる，無限に音程が上昇していくように聞こえる音があります．私も自分でその音を作ってみたいと思い，ちょっと勉強しました．とはいえ，まだ素人ですので，間違いがあれば指摘してください．完成した音をYoutubenにアップしておきました．

www.youtube.com

　いくつかのホームページの説明を読みましたが，仕組みを理解できませんでした．オリジナル論文が，私にはわかりやすかったです．その論文はが，これです．
[Shepard, Roger N. (1964). “Circularity in Judgements of Relative Pitch”. Journal of the Acoustical Society of America 36: 2346–53. doi:10.1121/1.1919362]

　音作りのポイントは，以下です．

オクターブ違いの音を複数並べて，基本周波数を上昇させる．

　1オクターブは，周波数で表せば2倍になります．例えば，基本周波数 (一番低い音)が50 Hzの場合は，1オクターブ上が100 Hz，2オクターブ上が200Hzです．

基本周波数を， $f_{\rm min}$ とすれば，第 $c$ 倍音 (第 $c$ 高調波)の周波数は，

　 $f^{(c)} = f_{\rm min} \cdot 2^{c-1}$

となります (下のRスクリプトのcは，1引いた値です)．ここで，倍音の最大値を $c_{\rm max}$ として， $c = 1, 2, 3, \cdots, c_{\rm max}$ です．

　さらに，それぞれの周波数を時間経過 $t$ と共に増加させ，時間幅 $t_{\rm max}$ で1オクターブ (2倍)上昇するために，

　 $f^{(c)}(t) = f_{\rm min} \cdot 2^{\left(c-1+t/t_{\rm max}\right)}$

とします．

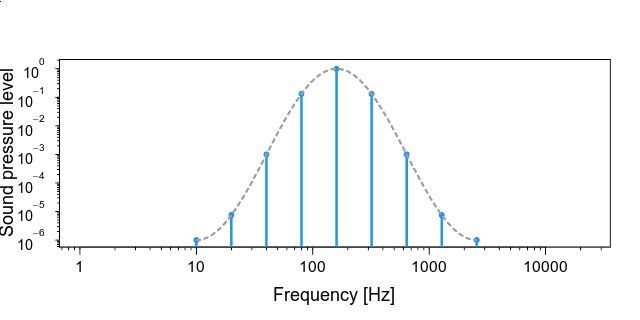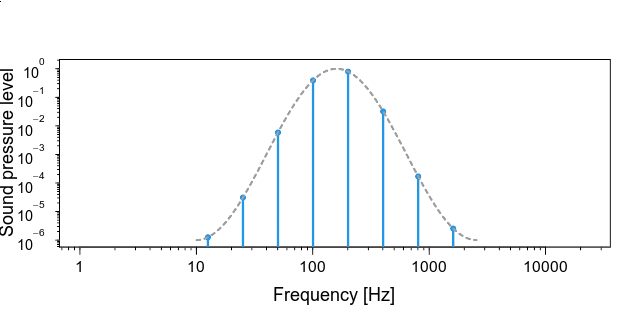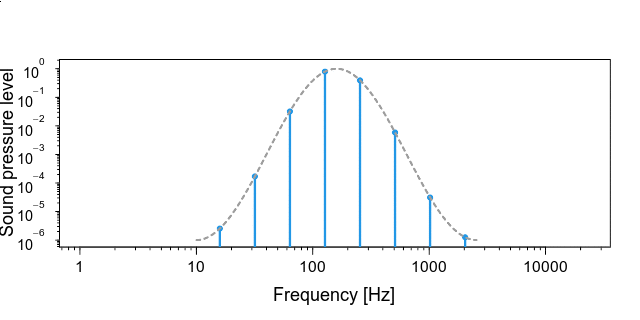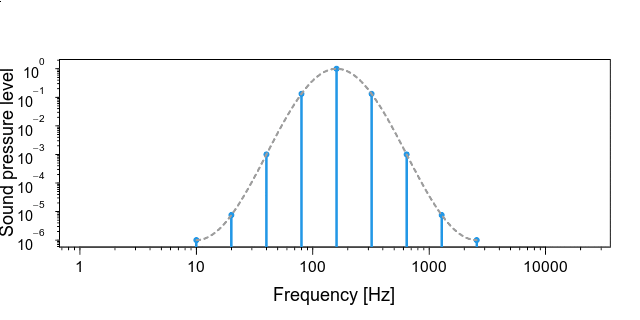
低音側と高音側でだんだんと音が小さくなるように決まったエンベロープの音圧バランスにする (ここが，数式を使わずに文章で説明するのが難しいです)．下の図は，横軸も縦軸も対数になっていることに注意してください．ぱっと見，グラフは

　 $\displaystyle \frac{1-\cos x}{2} \quad$ ( $0 \le x \le 2 \pi$ )

にするのですが，実際は，縦軸，横軸とも対数をとった後に，この形のエンベロープにします．しかも，幅も数オクターブの幅にする必要があります．

　まず，横軸について考えます． $f_{\rm min}$ が， $x=0$ に対応し， $f^{(c_{\rm max})}$ が， $x=2 \pi$ に対応するように，対数関数を作るとすれば，

　 $\displaystyle x = \frac{2 \pi}{c_{\rm max}} \log_{2} \left(\frac{f^{(c)}(t)}{f_{\rm min}} \right)$

になります．これを，指数の肩に載せれば，図のようなエンベロープが作れます．音圧レベルを $[L_{\rm min}, L_{\rm max}]$ の領域にする場合，周波数 $f^{(c)}(t)$ を持つ成分の振幅を，

　 $\displaystyle A^{(c)} (t) = 10^{L_{\rm min} + (L_{\rm max}- L_{\rm min}) (1-\cos x)/2}$

とします．ここで，

　 $\displaystyle x = \frac{2 \pi}{c_{\rm max}} \log_{2} \left(\frac{f^{(c)}(t)}{f_{\rm min}} \right)$

です．

　重要なのは，下のgifアニメのように，一番高い音が聞こえなくなるのにあわせて，低い音が聞こえはじめることのようです (青い棒がゆっくり動いてますよ)．

時間変化する周波数 $f(t)$ を持つ信号 $x(t)$ は，

　 $\displaystyle x(t) = A \sin \left(2 \pi f(t) t \right)$

で計算できない．ここで， $A$ は振幅です．正しいのは，

周波数が，時間に依存するとき関数 $f(t)$ のとき，振動は

　 $\displaystyle x(t) = A \sin \left(2 \pi \int_{\tau = 0}^t f(\tau) \, d\tau \right)$

ではないでしょうか．私は，このことにしばらく気づけませんでした．周波数は，振動の位相の進む早さを特徴付けているので， $\Delta t$ 刻みの離散時刻 $t_i = (i-1) \Delta t$ に， $\Delta t$ だけ時間が経過すると，位相 (角度)は

　 $\displaystyle \Delta \theta = 2 \pi f(t_i) \, \Delta t$

だけ進みます．注目すべきは時計の針の位置 (アナログ時計の針ですよ)なので，時刻 $t_i$ の位相 (角度)は，

　 $\displaystyle \theta (t_i) = \sum_{k=0}^{i} 2 \pi f(t_k) \, \Delta t$

で，これは，

　 $\displaystyle \theta (t_i) = \sum_{k=0}^{i} 2 \pi f(t_k) \, \Delta t \neq 2 \pi f(t_i) \, t_i = 2 \pi f(t_i) (i-1) \Delta t$

です．

　ということで，詳しく説明するのが面倒になったので，サンプルのRスクリプトを掲載しておきます．

Rスクリプト

# サンプリング周波数f.s
f.s <- 48000
dt <- 1/f.s
#################
# 時間依存する周波数を決める関数
freq <- function(time,c,f.min=20,t.max = 60){
  return(f.min*2^(c+time/t.max))
}
#################
# 生成する長さ
T <- 30
#
time <- seq(0,T,dt)
n.time <- length(time)
#################
# 最低周波数
f.min <- 10
# オクターブ(倍音)の数
c.max <- 8
#################
# -4の部分は生成する長さ/t.maxを参考に変更してください
c.list <- (-4):c.max
f.cut <- f.min*2^(c.max)
dB.min <- -120
##########################
for(i in 1:length(c.list)){
 f <- freq(time,c.list[i],f.min=10,t.max = 10)
 A <- 10^((dB.min-dB.min*(1-cos(2*pi/c.max*log(f/f.min)/log(2)))/2)/20)
 A[f > f.cut | f < f.min] <- 0
 #############################
 delt <- 2*pi*f/f.s
 theta <- cumsum(delt)-delt[1]
 x.sub <- A*sin(theta)
 #############################
 if(i == 1){
  x <- x.sub
 }else{
  x <- x + x.sub
 }
}
# xが信号データです．
# 音として保存すればシェパード・トーンを聴くことができます．