【Rで時系列解析】コヒーレンス (coherence)の計算 - ケィオスの時系列解析メモランダム

今回は，コヒーレンス (coherence，あるいは，magnitude-squared coherence)の計算のメモです．コヒーレンスは，2つの時系列間の相関を周波数領域で見る方法です．2つの信号の周波数成分に，線形な入出力関係があれば1に近くなります．なければ0です．とはいえ，入出力関係がなくても，2つの信号に同じ周波数の正弦波が含まれている場合も，その周波数で1に近くなります．

　今回のポイントは，「コヒーレンスを推定するときは，時系列を20以上の部分時系列に分けた方が良い」ということです．

コヒーレンスの推定結果 ( $a_{11}=0.6, a_{12}=0.3, a_{21}=-0.4, a_{22}=0.8$ )．長さ10,000の時系列を $n$ 個の部分区間に分けたとき．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

コヒーレンスの推定結果 ( $a_{11}=0.6, a_{12}=0.3, a_{21}=-0.4, a_{22}=0.8$ )．長さ10,000の時系列を $n$ 個の部分区間に分けたとき．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

コヒーレンス (coherence)の定義
クロススペクトルの推定
- 時系列を直接フーリエ変換する場合
- 相互共分散 (相互相関)関数をフーリエ変換する場合
数値実験
コヒーレンスの解釈
まとめと注意
Rスクリプト
- 時系列を直接フーリエ変換する場合
- 相互共分散 (相互相関)関数をフーリエ変換する場合

コヒーレンス (coherence)の定義

　2つの時系列 $x[t$ ]， $y[t$ ]について，それぞれのパワースペクトルの推定量を $\hat{S}_{xx} (f)$ ， $\hat{S}_{yy} (f)$ ，両者のクロススペクトルを $\hat{S}_{xy} (f)$ とします．このとき，コヒーレンスを次のように定義します．

　 $\displaystyle {\rm Coh} = \frac{\left| {\rm E} \left[ \hat{S}_{xy} (f) \right] \right|^2}{{\rm E} \left[ \hat{S}_{xx} (f) \right] {\rm E} \left[ \hat{S}_{yy} (f) \right]}$

ここで，期待値 ${\rm E}$ は，無限個のサンプル時系列についてとります．

　実際の時系列解析では，1本のサンプル時系列からコヒーレンスを推定したいと思います．そのときは，1本の時系列を複数の部分区間に分けて，それらの部分時系列について， $\hat{S}_{xx} (f)$ ， $\hat{S}_{yy} (f)$ ， $\hat{S}_{xy} (f)$ を計算し，周波数 $f$ ごとに，それぞれの平均を計算するのが一般的です．上の図は，部分区間の数で推定結果がどう変るかを表しています．たくさんの平均をとらないときれいになりません．

　今回は，50％オーバーラップで時系列を部分区間に分けて，コヒーレンスを推定します．以下では，前処理や後処理はしていません．実際には，お好みに合わせて，部分区間のトレンドを除いたり，平滑化したりしてください．

クロススペクトルの推定

　クロススペクトルも，通常のパワースペクトルと同じように，2つの方法で定義されます．一つは，時系列のフーリエ変換を使う方法，もう一つは，時系列の相互共分散 (相互相関)のフーリエ変換を使う方法です．パワースペクトルは実数ですが，クロススペクトルは複素数になることに注意してください．

時系列を直接フーリエ変換する場合

　2つの時系列 $x[t$ ]， $y[t$ ]のそれぞれの離散フーリエ変換を $X (f)$ ， $Y (f)$ とすれば，クロススペクトルの推定量は，

　 $\displaystyle \hat{S}_{xy} (f) = \frac{X(f) \overline{Y(f)}}{N}$

です．ここで， $\overline{Y(f)}$ は， $Y(f)$ の複素共役を表します．

相互共分散 (相互相関)関数をフーリエ変換する場合

　2つの時系列 $x[t$ ]， $y[t$ ]の相互共分散の推定量を $\hat{C}_{xy} (\tau)$ ( $-m \le \tau \le m$ )とすれば，クロススペクトルの推定量は，

　 $\displaystyle \hat{S}_{xy} (f) = \sum_{\tau = -m}^{m} \hat{C}_{xy} (\tau)\, e^{-i 2 \pi f \tau}$

です．

数値実験

　ここでは，簡単なモデルを仮定して，時系列を生成し，コヒーレンスを計算してみます．答えがないと，正しかどうか確かめられないので，解析的に計算したコヒーレンスと比較しました．

　モデルは，これです．

　 $\begin{equation} \left\{\begin{array}{l} x_t = a_{11} \, x_{t-1} + a_{12} \, y_{t-1} + \varepsilon^{(x)}_{t} \\ y_t = a_{21} \, x_{t-1} + a_{22} \, y_{t-1} + \varepsilon^{(y)}_{t} \\ \end{array}\right. \end{equation}$
　
ここで， $\varepsilon^{(x)}_{t}$ ， $\varepsilon^{(x)}_{t}$ は，それぞれ，分散 $\sigma_x^2$ ， $\sigma_y^2$ の白色ノイズで，お互いに相関がないとします．

　使ったスクリプトの例 (パラメタは違います)を最後に掲載しておきます．

コヒーレンスの推定結果 ( $a_{11}=0.6, a_{12}=0.4, a_{21}=0, a_{22}=0.8$ )．長さ100,000の時系列を1000個の部分区間に分けた．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

コヒーレンスの推定結果 ( $a_{11}=0.6, a_{12}=0.4, a_{21}=0, a_{22}=0.8$ )．長さ100,000の時系列を1000個の部分区間に分けた．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

コヒーレンスの推定結果 ( $a_{11}=0.6, a_{12}=0.3, a_{21}=-0.4, a_{22}=0.8$ )．長さ100,000の時系列を1000個の部分区間に分けた．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

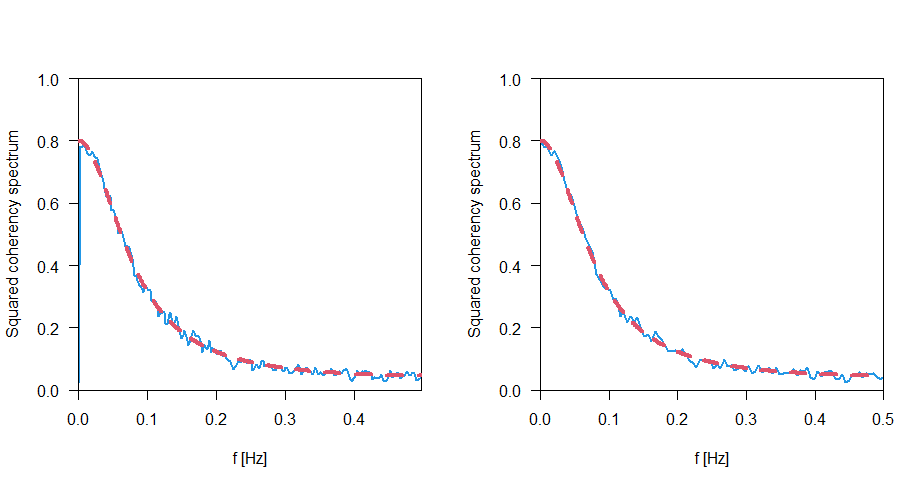
コヒーレンスの解釈

　コヒーレンスでは，2つの時系列の周波数成分について，両者の位相差を主に評価しています (振幅の影響も無視できない程度にありますが)．このことを，時系列のフーリエ変換を使った定義を使って説明します．

　2つの時系列 $x[t$ ]， $y[t$ ]のそれぞれの離散フーリエ変換を $X (f)$ ， $Y (f)$ とすれば，各周波数で，

　 $\begin{equation} \left\{\begin{array}{l} X (f) = A_x (f)\, e^{i \theta_x (f)} \\ Y (f) = A_y (f)\, e^{i \theta_y (f)} \\ \end{array}\right. \end{equation}$

と表すことができます．ここで， $A_x (f)=|X (f)|$ ， $A_y (f)=|Y (f) |$ です．

　もし，クロススペクトルの推定で複数のサンプルの平均値をとらなければ，コヒーレンスの計算結果は，

　 $\displaystyle \widehat{\rm Coh} = \frac{\left|A_x (f)\, e^{i \theta_x (f)}\, A_y (f)\, e^{-i \theta_y (f)} \right|^2}{|A_x (f)|^2 |A_y (f)|^2} = \left|e^{i(\theta_x(f)-\theta_y (f))} \right|^2 = 1$

と，必ず1になります．ですので，多数のサンプルの位相差を見なければ，意味のある結論はえられません．

　やや強引ですが， $A_x (f)$ と $A_y (f)$ の相関，さらに，振幅と位相差の相関を0と近似すれば，コヒーレンスは，

　 $\begin{eqnarray} {\rm Coh} &\approx& \left|{\rm E} \left[ e^{i(\theta_x(f)-\theta_y (f))} \right] \right|^2 \\ &=& \left|{\rm E} \left[ \cos \left\{\theta_x(f)-\theta_y (f) \right\} \right] + i \, {\rm E} \left[ \sin \left\{\theta_x(f)-\theta_y (f) \right\} \right]\right|^2\end{eqnarray}$

となります．フルで推定したコヒーレンスと，このように位相差だけで近似したコヒーレンスを数値的に比較した結果が下図です．位相差だけでも傾向は再現できています．

コヒーレンスを位相差だけで近似したとき．赤破線が解析的結果．青がフルでの推定結果．水色が位相差だけでの近似．

　位相差のみを使ったコヒーレンスの近似式は，複素平面上の単位円の円周上に位相差に対応する点をとり，それらの平均値を計算しています．そして，原点からの距離の2乗がコヒーレンスの値です．下の図は，位相差が完全にランダムな場合 (真のコヒーレンスが0)と，位相差に傾向がある場合 (真のコヒーレンスが0でない)について，位相差の平均値 (×印)位置のサンプル数 $n$ 依存性を表しています． $n$ は平均を計算するサンプル数です．複素平面上で，位相差の平均値が原点にあるということが，コヒーレンスが0であることに対応します．これは，角度データの統計学 (方位統計学)のアプローチと同じです．

コヒーレンスの計算における位相差 (●)の分布．×印は位相差の平均値を表す． $n$ は平均を計算するサンプル数．（左）コヒーレンスが0の例．サンプル数 $n$ が少ないと，平均値 (×印)が原点から大きくずれる．（右）コヒーレンスが0でない例．サンプル数 $n$ が増えても，平均値 (×印)が原点に近づかない．

　上図左では，サンプル数 $n$ が少ない場合 (10点以下)，真のコヒーレンスが0であっても，平均値 (×印)は原点から大きく外れています．しかし，サンプル数 $n$ が増えれば，平均値 (×印)は原点に近づいていきます．一方，上図右では，位相差が45°付近を中心にばらついており，サンプル数 $n$ が増えても，その平均値 (×印)は原点から外れたままです．

　ということで，コヒーレンスは，2つの時系列に含まれる周波数成分の位相差に一定の傾向があるかどうかを主に評価しています．主にといっているのは，振幅の関係性も実際は含まれるということです．下の図は，無相関な2つの時系列のコヒーレンスの推定結果です．平均をとるサンプル数 $n$ が小さいと，コヒーレンスが0にならない理由がわかりますか？

無相関な2つの時系列のコヒーレンス． $n$ は平均を計算するサンプル数．（左）相互共分散関数をフーリエ変換してクロススペクトルを推定した場合．(右) 時系列のフーリエ変換を使ってクロススペクトルを推定した場合．赤破線は，解析的に計算したコヒーレンス．

まとめと注意

　おそらく，正しくコヒーレンスを計算できています．

　実際の時系列からコヒーレンスを推定する場合，20以上の部分区間に分けた方が良いと思います．10では少ないと思います．時系列の長さが数100点の場合も，周波数の解像度を欲張らずに20分割くらいしてください．

　コヒーレンスでは，グレンジャー因果性のような，因果の向きは評価できません．実際の時系列解析では，相関があるのかどうかという基準を知りたいと思います．いろんな流儀があるようですが，私は，無関係な時系列を分析した結果と比較して，コヒーレンスの大小を議論することが多いです．因果性については，以下の記事も参考にしてください．

chaos-kiyono.hatenablog.com

Rスクリプト

時系列を直接フーリエ変換する場合

# データ長
N <- 10000
##################
# スペクトルの推定に使う部分区間の数
n.div <- 200
##################
# AR係数
# x[i] = a.11*x[i-1] + a.12*y[i-1] + w1[i] 
# y[i] = a.21*x[i-1] + a.22*y[i-1] + w2[i] 
a.11 <- 0.6
a.12 <- 0.4
a.21 <- -0.4
a.22 <- 0.8
sig2.1 <- 1
sig2.2 <- 1
##################
# サンプル時系列の生成
x <- c()
y <- c()
##################
w1 <- rnorm(N,0,sqrt(sig2.1))
w2 <- rnorm(N,0,sqrt(sig2.2))
x[1] <- w1[1]
y[1] <- w2[1]
for(i in 2:N){
 x[i] <- a.11*x[i-1]+a.12*y[i-1]+w1[i]
 y[i] <- a.21*x[i-1]+a.22*y[i-1]+w2[i] 
}
##################
n.sub2 <- floor(N/(n.div+1))
n.sub <- 2*n.sub2
i.sub <- seq(1,N,n.sub2)
x.sub <- c()
y.sub <- c()
##################
Sxy.est <- c()
Sxx.est <- c()
Syy.est <- c()
##################
for(i in 1:n.div){
 x.sub <- x[i.sub[i]:(i.sub[i]+n.sub-1)]
 y.sub <- y[i.sub[i]:(i.sub[i]+n.sub-1)]
 # fft
 X.sub <- fft(x.sub)
 Y.sub <- fft(y.sub)

 if(i == 1){
  # スペクトルの推定
  Sxy2.est <- data.frame(Sxy2=X.sub*Conj(Y.sub)/N)
  Sxx.est <- data.frame(Sxx=abs(X.sub)^2/N)
  Syy.est <- data.frame(Syy=abs(Y.sub)^2/N)
 }else{
  # スペクトルの推定
  Sxy2.est <- cbind(Sxy2.est,data.frame(Sxy2=X.sub*Conj(Y.sub)/N))
  Sxx.est <- cbind(Sxx.est,data.frame(Sxx=abs(X.sub)^2/N))
  Syy.est <- cbind(Syy.est,data.frame(Syy=abs(Y.sub)^2/N))
 }
}
# ２乗コヒーレンス
Coh.est <- abs(rowMeans(Sxy2.est))^2/(abs(rowMeans(Sxx.est))*abs(rowMeans(Syy.est)))
freq <- c((0:(n.sub-1))/(n.sub))
##################
par(mfrow=c(1,1))
plot(freq[freq<=0.5],Coh.est[freq<=0.5],"l",col=4,lwd=2,xaxs="i",ylim=c(0,1),xlab="f [Hz]",ylab="Squared coherency spectrum",las=1,yaxs="i")


##################################################################
# 解析的スペクトルを使った計算
# AR係数の行列
A <- matrix(c(a.11,a.12,a.21,a.22),nrow=2,ncol=2,byrow=TRUE)
# 単位行列
I <- diag(2)
###
# 周波数の点数(描画のためのfを何点とるか)
n <- 500
f.list <- seq(0,0.5,length.out=n)
###
Sx <- c()
Sy <- c()
Sx0 <- c()
Sy0 <- c()
Sxy <- c()
for(j in 1:n){
 f <- f.list[j]
 z <- exp(2*pi*f*1i)
 # 逆行列
 B <- solve(I-A*z)
 # スペクトルの計算
 Sx[j] <- B[1,1]*Conj(B[1,1])*sig2.1+B[1,2]*Conj(B[1,2])*sig2.2
 Sx0[j] <- B[1,1]*Conj(B[1,1])*sig2.1
 Sy[j] <- B[2,1]*Conj(B[2,1])*sig2.1+B[2,2]*Conj(B[2,2])*sig2.2
 Sy0[j] <- B[2,2]*Conj(B[2,2])*sig2.2
 Sxy[j] <- B[1,1]*Conj(B[2,1])*sig2.1+B[1,2]*Conj(B[2,2])*sig2.2
}
# ２乗コヒーレンス
Coh.ana <- abs(Sxy)^2/(Re(Sx)*Re(Sy))
lines(f.list,Coh.ana,col=2,lwd=4,lty=2)

相互共分散 (相互相関)関数をフーリエ変換する場合

# データ長
N <- 10000
##################
# スペクトルの推定に使う部分区間の数
n.div <- 200
##################
# AR係数
# x[i] = a.11*x[i-1] + a.12*y[i-1] + w1[i] 
# y[i] = a.21*x[i-1] + a.22*y[i-1] + w2[i] 
a.11 <- 0.6
a.12 <- 0.4
a.21 <- 0
a.22 <- 0.8
sig2.1 <- 1
sig2.2 <- 1
##################
# サンプル時系列の生成
x <- c()
y <- c()
##################
w1 <- rnorm(N,0,sqrt(sig2.1))
w2 <- rnorm(N,0,sqrt(sig2.2))
x[1] <- w1[1]
y[1] <- w2[1]
for(i in 2:N){
 x[i] <- a.11*x[i-1]+a.12*y[i-1]+w1[i]
 y[i] <- a.21*x[i-1]+a.22*y[i-1]+w2[i] 
}
##################
n.sub2 <- floor(N/(n.div+1))
n.sub <- 2*n.sub2
i.sub <- seq(1,N,n.sub2)
x.sub <- c()
y.sub <- c()
##################
Sxy.est <- c()
Sxx.est <- c()
Syy.est <- c()
##################
# 最大ラグ
m <- n.sub-1
##################
for(i in 1:n.div){
 x.sub <- x[i.sub[i]:(i.sub[i]+n.sub-1)]
 y.sub <- y[i.sub[i]:(i.sub[i]+n.sub-1)]
 # 相互共分散の推定
 Cxy <- ccf(x.sub,y.sub,lag=m,plot=FALSE,type="covariance")$acf[,1,1]
 #　自己共分散の推定
 Cxx <- acf(x.sub,lag.max=m,plot=FALSE,type="covariance")$acf[,,1]
 Cyy <- acf(y.sub,lag.max=m,plot=FALSE,type="covariance")$acf[,,1]
 if(i == 1){
  # スペクトルの推定
  Sxy2.est <- data.frame(Sxy2=fft(Cxy))
  Sxx.est <- data.frame(Sxx=fft(c(Cxx,rev(Cxx[-1]))))
  Syy.est <- data.frame(Syy=fft(c(Cyy,rev(Cyy[-1]))))
 }else{
  # スペクトルの推定
  Sxy2.est <- cbind(Sxy2.est,data.frame(Sxy2=fft(Cxy)))
  Sxx.est <- cbind(Sxx.est,data.frame(Sxx=fft(c(Cxx,rev(Cxx[-1])))))
  Syy.est <- cbind(Syy.est,data.frame(Syy=fft(c(Cyy,rev(Cyy[-1])))))
 }
}
# ２乗コヒーレンス
Coh.est <- abs(rowMeans(Sxy2.est))^2/(abs(rowMeans(Sxx.est))*abs(rowMeans(Syy.est)))
freq <- c((0:(n.sub-1))/(2*n.sub),-((n.sub-1):1)/(2*n.sub))
##################
par(mfrow=c(1,1))
plot(freq[freq>=0],Coh.est[freq>=0],"l",col=4,lwd=2,xaxs="i",ylim=c(0,1),xlab="f [Hz]",ylab="Squared coherency spectrum",las=1,yaxs="i")

##################################################################
# 解析的スペクトルを使った計算
# AR係数の行列
A <- matrix(c(a.11,a.12,a.21,a.22),nrow=2,ncol=2,byrow=TRUE)
# 単位行列
I <- diag(2)
###
# 周波数の点数(描画のためのfを何点とるか)
n <- 500
f.list <- seq(0,0.5,length.out=n)
###
Sx <- c()
Sy <- c()
Sx0 <- c()
Sy0 <- c()
Sxy <- c()
for(j in 1:n){
 f <- f.list[j]
 z <- exp(2*pi*f*1i)
 # 逆行列
 B <- solve(I-A*z)
 # スペクトルの計算
 Sx[j] <- B[1,1]*Conj(B[1,1])*sig2.1+B[1,2]*Conj(B[1,2])*sig2.2
 Sx0[j] <- B[1,1]*Conj(B[1,1])*sig2.1
 Sy[j] <- B[2,1]*Conj(B[2,1])*sig2.1+B[2,2]*Conj(B[2,2])*sig2.2
 Sy0[j] <- B[2,2]*Conj(B[2,2])*sig2.2
 Sxy[j] <- B[1,1]*Conj(B[2,1])*sig2.1+B[1,2]*Conj(B[2,2])*sig2.2
}
# ２乗コヒーレンス
Coh.ana <- abs(Sxy)^2/(Re(Sx)*Re(Sy))
lines(f.list,Coh.ana,col=2,lwd=4,lty=2)