前回,振動している信号のエンベロープ (包絡線)をヒルベルト変換で求める方法を紹介しました.今回は,この方法がうまくいくための注意事項をいくつか書いておきます.
ポイントは,
前処理として,周波数の狭いバンドパスをかけておく
あるいは
前処理として,Emprical Mode Decomposition (EMD)で時系列を分解しておく
ということです.
バンドパスも,EMDも,私の記事では説明したことはありません.今回の内容は,これらを学ぶきっかけにしてください.
前回の記事はこれです.
chaos-kiyono.hatenablog.com
ゼロの上下に同じくらいの振幅で振動する必要がある
ヒルベルト変換は,0を中心としてバランス良く振動している成分だとうまくいきます.下の図では,元信号のベースラインを0から上にずらしたときに,ヒルベルト変換で計算されるエンベロープがどうなるかを描いています.

端っこの影響を受ける
ヒルベルト変換の計算でフーリエ変換を使っているので,端っこが0に近づいていない,あるいは,元信号を繰り返しつなげたときにきれいにつながっていないと,想定外の周期が出現します.フーリエ変換って,結局,フーリエ級数と同じです.

主役の周波数は一つ
局所的に,周期が異なる複数の振動が含まれていると,うまくいきません.下の図は,周期が異なる2つの振動が含まれる信号のエンベロープを計算した例です.
下の図は,白色ノイズのエンベロープを計算した例です.

主役周波数が一つであれば,周波数は変っても構わない
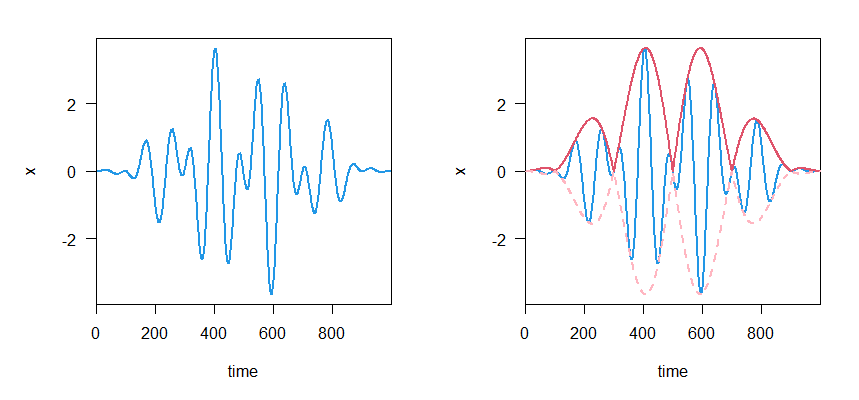
周波数が変化する場合も,主役の振動成分が一つであれば,エンベロープを計算できます.下の図では,周波数を連続的に大きくしてあります.エンベロープはきれいに求まっています.

Rスクリプト
使ったRスクリプトを一部載せておきます.
############################## # サンプル時系列の生成 # 時系列の長さ N <- 1000 # サンプリング間隔1で時間を定義 time <- 0:(N-1) # 振動の総回数 n.osci1 <- 2 n.osci2 <- 8 omega <- exp(seq(log(2*pi/(N/n.osci1)),log(2*pi/(N/(10*n.osci2))),length.out=N)) x <- (1-cos(2*pi*time/(N-1)))*sin(cumsum(omega)) ############################### # Hilbert変換 # 周波数を定義 f <- (0:(N-1))/N f[f > 1/2] <- f[f > 1/2]-1 ### # xをフーリエ変換 X <- fft(x) # Xの各周波数の位相を90°ずらす X.H <- 1i*sign(f)*X # フーリエ逆変換して振動成分の虚部をえる x.h <- Re(fft(X.H,inverse=TRUE))/N ### # ヒルベルト変換の結果 # 虚部の値x.hをもとの信号xに加える z <- x+1i*x.h # 振幅 amp <- abs(z) ################################ # プロット par(mfrow=c(1,2),pty="m") plot(time,x,"l",col=4,lwd=2,las=1,xaxs="i",xlab="time",ylab="x",xlim=c(0,N-1)) plot(time,x,"l",col=4,lwd=2,las=1,xaxs="i",xlab="time",ylab="x",xlim=c(0,N-1)) # 上のエンベロープ lines(time,amp,"l",col=2,lwd=2) # 下のエンベロープ lines(time,-amp,"l",col="lightpink",lty=2,lwd=2)