【Rで時系列解析】コサイナー解析 (cosinor analysis) - ケィオスの時系列解析メモランダム

ひさびさに，共同研究でコサイナー解析 (cosinor analysis)を頼まれたので，ポイントをメモっておきます．コサイナー解析というのは，周期的に変化すると思われる時系列に，コサインの波形を当てはめてる分析法です．概日リズムの特徴付けに使われることがあります．Rでは，"cosinor"パッケージがあります．ただし，このパッケージの結果では位相が180°ずれることがあるので，結果の解釈には注意が必要です．ここでは，自作のRスクリプトを下に載せておきました．

周期回帰モデルの当てはめ
Rスクリプト

周期回帰モデルの当てはめ

　コサイナー解析では周期 $T$ を既知として，以下のモデルを仮定します．

　 $\displaystyle y(t) = \mu + A \cos \left(\frac{2 \pi t}{T} - \phi \right) + \varepsilon(t)$

ここで， $\mu$ は，MESOR (midline statistic of rhythm)， $A$ は振幅， $\phi$ はacrophase (頂点位相)と呼ばれるパラメタです． $\varepsilon(t)$ は，ランダムな要因やその他の変動を表します．

　観測されて時系列から， $\varepsilon(t)$ の２乗和が最小になるように， $\mu$ ， $A$ ， $\phi$ を推定します．そのために，

　 $\begin{eqnarray} y(t) &=& \mu + A \cos \left(\frac{2 \pi t}{T} - \phi \right) + \varepsilon(t) \\ &=& \mu + A \cos \phi \, \cos \left(\frac{2 \pi t}{T} \right) + A \sin \phi \, \sin \left(\frac{2 \pi t}{T} \right) + \varepsilon(t) \end{eqnarray}$

と変形します．ここで，

　 $\beta= A \cos \phi$ ， $\gamma = A \sin \phi$

　 $\displaystyle x(t) = \cos \left(\frac{2 \pi t}{T} \right)$ ， $\displaystyle z(t) = \sin \left(\frac{2 \pi t}{T} \right)$

とおけば，

　 $\begin{eqnarray} y(t) &=& \mu + A \cos \phi \, \cos \left(\frac{2 \pi t}{T} \right) + A \sin \phi \, \sin \left(\frac{2 \pi t}{T} \right) + \varepsilon(t) \\ &=& \mu + \beta \, x(t) + \gamma \, z(t) + \varepsilon(t) \\ \end{eqnarray}$

となります．

　 $N$ 点の観測データ $\left\{ y(t_1), y(t_2), \cdots, y(t_N) \right\}$ がえられたとき，まず， $\mu$ ， $\beta$ ， $\gamma$ を推定すると，

　　 $\begin{eqnarray} \begin{bmatrix} \displaystyle \sum_{i=1}^{N} y(t_i) \\ \displaystyle \sum_{i=1}^{N} y(t_i)\, x(t_i)\\ \displaystyle \sum_{i=1}^{N} y(t_i)\, z(t_i)\\ \end{bmatrix} &=& \begin{bmatrix} N & \displaystyle \sum_{i=1}^{N} x(t_i) & \displaystyle \sum_{i=1}^{N} z(t_i) \\ \displaystyle \sum_{i=1}^{N} x(t_i) & \displaystyle \sum_{i=1}^{N} x(t_i)^2 & \displaystyle \sum_{i=1}^{N} x(t_i)\, z(t_i) \\ \displaystyle \sum_{i=1}^{N} z(t_i) & \displaystyle \sum_{i=1}^{N} x(t_i)\, z(t_i) & \displaystyle \sum_{i=1}^{N} z(t_i)^2 \\ \end{bmatrix} \begin{bmatrix} \hat{\mu} \\ \hat{\beta} \\ \hat{\gamma} \\ \end{bmatrix} \\ \begin{bmatrix} \hat{\mu} \\ \hat{\beta} \\ \hat{\gamma} \\ \end{bmatrix} &=&\begin{bmatrix} N & \displaystyle \sum_{i=1}^{N} x(t_i) & \displaystyle \sum_{i=1}^{N} z(t_i) \\ \displaystyle \sum_{i=1}^{N} x(t_i) & \displaystyle \sum_{i=1}^{N} x(t_i)^2 & \displaystyle \sum_{i=1}^{N} x(t_i)\, z(t_i) \\ \displaystyle \sum_{i=1}^{N} z(t_i) & \displaystyle \sum_{i=1}^{N} x(t_i)\, z(t_i) & \displaystyle \sum_{i=1}^{N} z(t_i)^2 \\ \end{bmatrix}^{-1} \begin{bmatrix} \displaystyle \sum_{i=1}^{N} y(t_i) \\ \displaystyle \sum_{i=1}^{N} y(t_i)\, x(t_i)\\ \displaystyle \sum_{i=1}^{N} y(t_i)\, z(t_i)\\ \end{bmatrix} \end{eqnarray}$

となります．ここで，

　 $\displaystyle x(t_i) = \cos \left(\frac{2 \pi t_i}{T} \right)$ ， $\displaystyle z(t_i) = \sin \left(\frac{2 \pi t_i}{T} \right)$

であることを忘れないでください．また， $\hat{\mu}$ ， $\hat{\beta}$ ， $\hat{\gamma}$ に，ハットと呼ばれる飾りがついているのは，これらが，真の $\mu$ ， $\beta$ ， $\gamma$ ではなく，それらを推定した値だよという気持ちを表しています．

　 $\hat{\mu}$ ， $\hat{\beta}$ ， $\hat{\gamma}$ を推定したら，

　 $\begin{eqnarray} \hat{A}&=&\sqrt{\hat{\beta}^2+\hat{\gamma}^2} \\ \hat{\phi} &=& \arctan \left( \frac{\hat{\gamma}}{\hat{\beta}}\right)\end{eqnarray}$

と変換できます．この式だと， $\arctan$ の定義から， $- \pi/2 < \hat{\phi} < \pi/2$ と範囲が狭くなり，場合によって正しい $\hat{\phi}$ が推定できません (180°ずれる)．この問題を避けるために，実際の計算 (RやC言語など)では，atan2を使えば良いと思います (下記のRスクリプト参照)．

　このモデルの検定は，周期 $T$ の変動はないという帰無仮説を検証します．以下のRスクリプトでは，F検定の結果を計算しています．方法は，この論文

Cornelissen, G. (2014). Cosinor-based rhythmometry. Theoretical Biology and Medical Modelling, 11(1), 1-24.

に説明してあります．

Rスクリプト

　パッケージに頼らないバージョンです．

# 周期
T <- 24
# テスト用の数値データの生成
time <-  seq(0,24,1)
mesor <- 0
amp <- 2
phase <- 0
eps <- rnorm(length(time))
y <- mesor+amp*cos(2*pi*time/T-phase)+eps
#####################
# プロット
par(mfrow=c(1,1),pty="m")
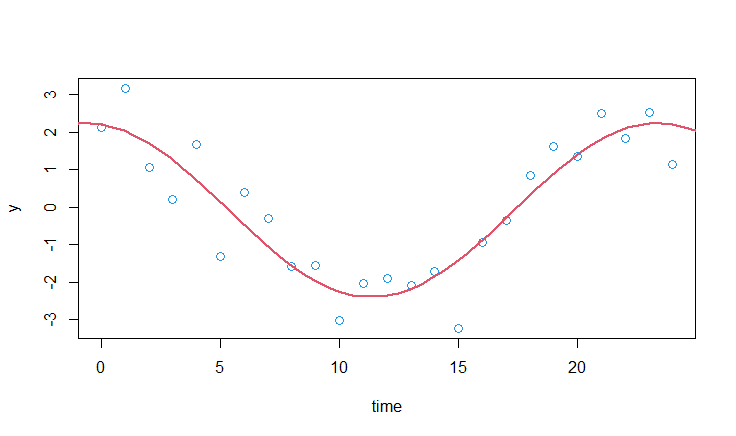
plot(time,y,xlab="time",col=4,cex=1.2)

##################################
# Cosinor解析
N <- length(y)
x <- cos(2*pi*time/T)
z <- sin(2*pi*time/T)
#
Y <- matrix(c(sum(y),sum(y*x),sum(y*z)),　ncol=1) 
X <- matrix(c(N,sx<-sum(x),sz<-sum(z),sx,sum(x^2),sxz<-sum(x*z),sz,sxz,sum(z^2)),ncol=3)
X.inv <- solve(X)
A <- X.inv %*% Y
#　モデルパラメタの推定結果
mesor.est <- A[1,1]
amp.est <- sqrt(A[2,1]^2+A[3,1]^2)
phase.est <- atan2(A[3,1],A[2,1])
# 当てはめ結果のプロット
curve(amp.est*cos(2*pi*x/T-phase.est)+mesor.est,xlim=c(min(time-12),max(time+12)),add=TRUE,col=2,lwd=2)
###################################
y.bar <- mean(y)
y.hat <- mesor.est+amp.est*cos(2*pi*time/T-phase.est)
###
MSS <- sum((y.hat-y.bar)^2)
RSS <- sum((y-y.hat)^2)
###
sig2.est <- RSS/(N-3)
F.stat <- (MSS/2)/sig2.est 
p.value <- 1-pf(F.stat,2,N-3)

TXT <- sprintf("MESOR = %f\nA = %f\nphi = %f\np = %f\n",mesor.est,amp.est,phase.est,p.value)
cat(TXT)

　"cosinor"パッケージというのもあります．ただし，このパッケージは， $\arctan$ の呪いが残っているので，位相が $\pi$ (180°)ずれた推定結果がでる場合があります．フィットの結果を見て，rrrがマイナスのときは，acrophaseに $\pi$ 足すか，引くか，自分でやってください．

# コサイナー解析（パッケージを使用）
# install.packages("cosinor")
require(cosinor)
###
# モデル当てはめ
cos.fit <- cosinor.lm(y~time(t), period = 24, data=data.frame(t=time,y=y))