【受動歩行の物理の基礎】角運動量の保存 - ケィオスの時系列解析メモランダム

受動歩行を単純化したモデルとしてリムレスホイールがあります．

今回は，リムレスホイールの運動を理解するために，ポイントとなる角運動量について解説します．

ポイントは，以下の3つです．

角運動量ベクトルの大きさは位置ベクトルと運動量ベクトルが作る平行四辺形の面積で，その向きは回転軸の右ネジ方向
回転していない並進運動でも角運動量は保存
回転の軸が変わっても角運動量は保存

質点の角運動量
並進運動でも角運動量は保存
回転の軸が変わっても角運動量は保存
まとめ

質点の角運動量

　まずは，質点の場合の角運動量の定義の確認です．

　上の図のように，運動量 ${\bf p}$ をもつ質点の原点Oまわりの角運動量 ${\bf L}$ は，質点の位置ベクトルを ${\bf r}$ として，

　 ${\bf L} = {\bf r} \times {\bf p}$

で与えられます．この式の $\times$ は外積を表しています．

　角運動量 ${\bf L}$ の大きさ $|{\bf L}|$ は， ${\bf r}$ と ${\bf p}$ を隣り合う2辺とする平行四辺形の面積になります．

角運動量の大きさは位置ベクトル ${\bf r}$ と運動量ベクトル ${\bf p}$ が作る平行四辺形の面積．

角運動量の大きさは位置ベクトル ${\bf r}$ と運動量ベクトル ${\bf p}$ が作る平行四辺形の面積．

　平行四辺形の面積は「底辺かける高さ」なので，上の図のように運動量ベクトルと平行な2直線の距離を $d$ とすれば，角運動量の大きさ $|{\bf L}|$ は，

　 $|{\bf L}| = d \, |{\bf p}|$

になります．この距離 $d$ を考えると，角運動量の大きさの計算は簡単です．

　角運動量の向きは，右ネジが進む回転方向になります．昔，私が工事現場で働きはじめたとき，ネジの構造を知らなかったので，回す方向が分からず，バカにされました．ネジは右に回すと締まるのは世界の常識です．逆ネジは特別な用途のみに使われるネジです．工事現場での仕事は非常に勉強になりました．

並進運動でも角運動量は保存

　回ってなくても，運動量があれば任意の点における角運動量は保存します．並進運動でも，角運動量が存在していることを忘れないでください．回転軸が固定されれば，その軸まわりの角運動量を考えてください．

　ここでは例として，下の図のように，無重力中を並進運動する円盤 (奥行きのある円柱)を考えます．この円盤は，点Aに衝突し，その後，点Aを回転軸として回転運動をはじめるとします．

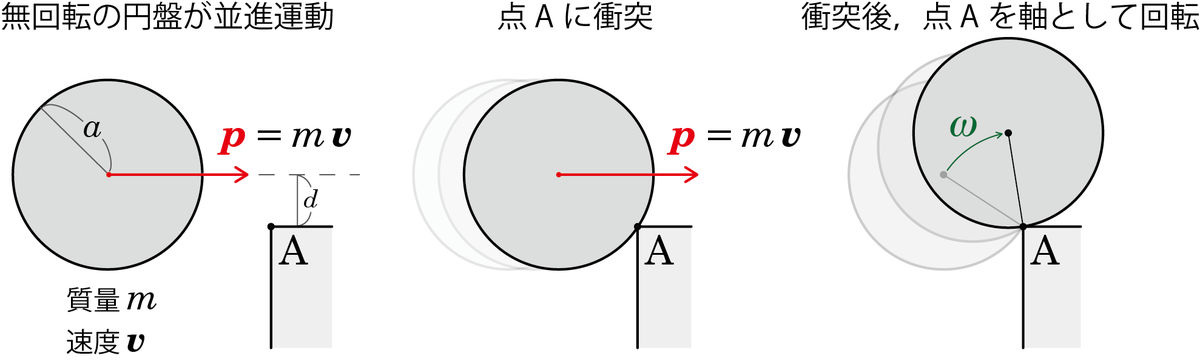
　上の状況では点Aにぶつかる直前まで，円盤は回転していません．回転していなくても，点Aまわりの角運動量は存在し，保存しています．位置ベクトルと運動量ベクトルを描いた下の図を見てください．

　角運動量の大きさは，位置ベクトルと運動量ベクトルが作る平行四辺形の面積なので，上の図の下のように面積は変わらず一定になることが分かります．

　点Aに衝突した後は，この角運動量が点Aまわりの回転運動の角運動量になります．下の図のように，衝突後の点Aまわりの角速度 $\omega$ を求めてみてください．

回転の軸が変わっても角運動量は保存

　下の図のように，回転の軸が突然変わる状況を考えてみます．

　ポイントは，回転軸が変わっても角運動量は保存するということです．私はアホなので，昔は，何で保存するのか理解できていない時期がありました．上の図の状況を考えて，角運動量を計算して，保存することを確認してみます．

　計算の流れは，円盤を微小部分に分けて，各微小部分の角運動量を求め，それを円盤全体で積分します．

　下の図のように，微小部分について，運動量ベクトルと平行な直線を回転軸を通るようにとり，運動量ベクトルと平行な2つの直線 (下図の破線)の距離を考えれば，角運動量の大きさが計算できます．

　円盤の質量を $m$ ，半径を $a$ とすれば，円盤の面密度 $\rho$ は，

　 $\displaystyle \rho = \frac{m}{\pi a^2}$

です．

　まず，微小部分について点Oまわりの角運動量の大きさ $dL$ を計算します．角運動量は，「(2本の平行線の距離)かける(密度)かける(面積)かける(速さ)」なので，

　 $\displaystyle dL = r \rho (r dr d\theta) ( r \omega) = \frac{m \omega}{\pi a^2} r^3 dr d \theta$
　
　円盤全体では，円盤の半径を $a$ として，

　 $\displaystyle |L| = \int_{r = 0}^{a} \! \int_{\theta=0}^{2 \pi} \! \frac{m \omega}{\pi a^2} r^3 dr d \theta = \frac{ma^2}{2} \omega$

円盤の慣性モーメントが，

　 $\displaystyle \frac{ma^2}{2}$

になることが分かるので，これで正しいと思います．

　次に，回転の中心を点Aに変更した瞬間を考えてみます．角運動量は，「(2本の平行線の距離)かける(密度)かける(面積)かける(速さ)」なので，変わるのは，2本の平行線の距離の部分です．上の図の右のように考えれば，2本の平行線の距離は， $r + a \sin \theta$ になることが分かります．微小部分について点Aまわりの角運動量の大きさ $dL$ は，

　 $\displaystyle dL = (r + a \sin \theta) \rho (r dr d\theta) ( r \omega) = \frac{m \omega}{\pi a^2} r^3 dr d \theta + \frac{m \omega}{\pi a} r^2 \sin \theta dr d \theta$