【Rで時系列解析】1次自己回帰過程のパワースペクトル - ケィオスの時系列解析メモランダム

今日のセミナーの課題は，以下です．
問題1　1次自己回帰過程の時系列サンプルを生成せよ．
　 $y_{n}=a y_{n-1} + w_n$
　ここで， $a$ は， $-1 < a < 1$ の定数， $w_n$ は，平均0，分散 $\sigma^2$ の白色ノイズである．
　 $a=0.99$ ， $\sigma^2=1$ とせよ．
問題2　1次自己回帰過程のパワースペクトルを推定せよ．100個の時系列サンプルのパワースペクトルを計算して，周波数毎に平均をとること．
　パワースペクトルの推定量は， $\hat{S}(f_k)= \displaystyle \frac{1 }{N} \left|\sum_{n=0}^{N-1} y_n \, e^{- i 2 \pi f_k n} \right|^2$ $\displaystyle \left(f_k = \frac{k}{N}\right)$ と，教科書の定義（自己共分散関数のフーリエ変換）の2つの方法を使い，結果を比較すること．
問題3　1次自己回帰過程のパワースペクトルの理論曲線（解析的に求めた結果）と，上で計算したパワースペクトル（数値的に求めた結果）のグラフを重ねて描け．

時系列の生成

Rで時系列を再生するスクリプトはこんな感じです．

# 1次自己回帰過程 (first-order autoregressive process) AR(1)の数値実験
# y[n] = a y[n-1] + w[n]
# w[n]: white noise with zero mean and variance sig^2
####################
# パラメタ (parameter)
a <- 0.9
# sig^2
sig2 <- 9
# 時系列の長さ
N <- 10000
####################
# 白色ノイズの生成 
w <- rnorm(N,0,sqrt(sig2))
####################
# 空の変数を事前に準備
y <- c()
# 初期値をy[1]=w[1]とする
y[1] <- w[1]
for(n in 2:N){
 y[n] <- a*y[n-1]+w[n]
}
# グラフを描いてみる
plot(1:N,y,"l",xlab="n",ylab="y[n]",col=4,xaxs="i",main=paste("AR(1) with a = ",a))

時系列からパワースペクトル（ペリオドグラム）の推定

1本の時系列データからパワースペクトルを推定するのは，こんな感じ（理論的なパワースペクトルを赤破線で重ね書きしています）．以下では， $\hat{S}(f_k)= \displaystyle \frac{1 }{N} \left|\sum_{n=0}^{N-1} y_n \, e^{- i 2 \pi f_k n} \right|^2$ を使ってパワースペクトルを推定しています．

######################
# Fast Fourier Transform (FFT)
# (Rを信じてのfftコマンドを使います)
Y.fft <- fft(y)
PSD <- abs(Y.fft)^2/N
######################
par(mfrow=c(3,2))
par(cex.axis=1.2,cex.lab=1.4)
######################
# FFTの結果をそのままグラフにすると
# 周波数は，f_k = k/n
freq <- (1:N-1)/N
plot(freq,PSD,"l",col=4,main="linear plot",xlab="f",xaxs="i")
plot(freq,PSD,"l",col=4,log="y",main="semi-log plot",xlab="f",yaxt="n",xaxs="i")
# 対数目盛を描く
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
###
# Nyquist周波数の
freq[freq>0.5] <- freq[freq>0.5]-1
PSD <- PSD[order(freq)]
freq <- freq[order(freq)]
plot(freq,PSD,"l",col=4,main="linear plot",xlab="f",xaxs="i")
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)
###############
plot(freq,PSD,"l",col=4,log="y",main="semi-log plot",xlab="f",yaxt="n",xaxs="i")
# 対数目盛を描く
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)
###############
f <- freq[freq>=0 & freq<=0.5]
S.f <- PSD[freq>=0 & freq<=0.5]
plot(f,S.f,"l",col=4,main="linear plot",xlab="f",xaxs="i")
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)
###############
plot(f[-1],S.f[-1],"l",col=4,log="xy",main="log-log plot",xlab="f",xaxt="n",yaxt="n",xaxs="i")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)

自己共分散からパワースペクトルを推定（Blackman-Tuley法）

自己共分散からパワースペクトルを推定するのは，こんな感じ（理論的なパワースペクトルを赤破線で重ね書きしています）．日野幹雄先生の「スペクトル解析」（朝倉書店）pp. 186-187を参考にしました．平滑化しないと，パワースペクトルが負になるので，自信はありません．ミスを見つけたら教えてください．

# 最大ラグの決定　（yを時系列とする）
m <- round(length(y)/4)
# 自己共分散の推定 (sample autocovariance)
a.cov <- acf(y,lag.max=m,type="covariance",plot=FALSE)$acf[,,1]
####################
# 周波数の定義
freq <- (0:m)/(2*m)
PSD0 <- c()
PSD <- numeric(m+1)
v.acov <- c(a.cov[1],2*a.cov[2:m],a.cov[m+1]) 
for(i in 1:(m+1)){
 v.cos <- cos((i-1)*(0:m)*pi/m)
 PSD0[i] <- v.acov %*% v.cos 
}
####################
# 平滑化（これがないと，スペクトルがマイナスになることがあります）
PSD[2:m] <- PSD0[2:m]*0.5+0.25*PSD0[1:(m-1)]+0.25*PSD0[3:(m+1)]
PSD[1] <- (PSD0[1]+PSD0[2])/2
PSD[m+1] <- (PSD0[m]+PSD0[m+1])/2
######################
par(mfrow=c(1,2))
par(cex.axis=1.2,cex.lab=1.4)
######################
# プロット
plot(freq,PSD,"l",col=4,main="linear plot",xlab="f",xaxs="i")
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)
####################
plot(freq[-1],PSD[-1],"l",col=4,log="xy",main="log-log plot",xlab="f",xaxt="n",yaxt="n",xaxs="i")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2)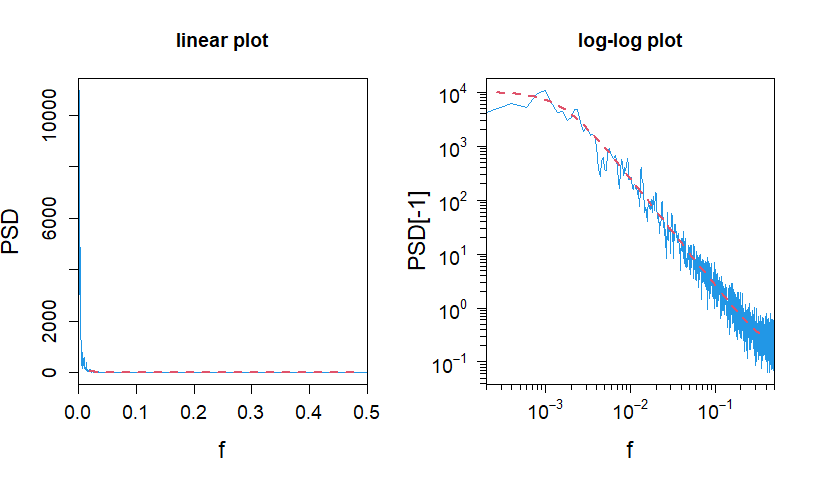

サンプル時系列を増やして平均スペクトルの計算

たくさんの標本時系列からパワースペクトルを計算する場合は，以下のRスクリプトを参考にしてください（以下では，a=0.9としてある）．まずは，時系列からパワースペクトルを推定した場合．

# 1次自己回帰過程 (first-order autoregressive process) 
# y[n] = a y[n-1] + w[n]
# w[n]: white noise with zero mean and variance sig^2
####################
# パラメタ (parameter)
a <- 0.9
# sig^2
sig2 <- 1
# 時系列の長さ
N <- 10000
####
y <- c()
####################
# 平均をとるサンプル時系列数
N.samps <- 100 
####################
for(ii in 1:N.samps){
 ####################
 # 白色ノイズの生成 
 w <- rnorm(N,0,sqrt(sig2))
 ####################
 # 空の変数を事前に準備
 # 初期値をy[1]=w[1]とする
 y[1] <- w[1]
 for(n in 2:N){
  y[n] <- a*y[n-1]+w[n]
 }
 ######################
 Y.fft <- fft(y)
 PSD <- abs(Y.fft)^2/N
 freq <- (1:N-1)/N
 freq[freq>0.5] <- freq[freq>0.5]-1
 PSD <- PSD[order(freq)]
 freq <- freq[order(freq)]
 ######################
 S.f <- PSD[freq>=0 & freq<=0.5]
 if(ii == 1){
  PSD.samps <- data.frame(S.f)
 }else{
  PSD.samps <- cbind(PSD.samps,data.frame(S.f))
 }
}
f <- freq[freq>=0 & freq<=0.5]
Spec <- rowMeans(PSD.samps)


###############
plot(f[-1],Spec[-1],"l",col=4,log="xy",main="log-log plot",xlab="f",xaxt="n",yaxt="n",xaxs="i",ylab="Spectrum")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2,n=1000)

次は，自己共分散を使ってパワースペクトルを推定した場合．

# 1次自己回帰過程 (first-order autoregressive process) 
# y[n] = a y[n-1] + w[n]
# w[n]: white noise with zero mean and variance sig^2
####################
# パラメタ (parameter)
a <- 0.9
# sig^2
sig2 <- 1
# 時系列の長さ
N <- 10000
####
y <- c()
####################
# 平均をとるサンプル時系列数
N.samps <- 100
####################
# 最大ラグの決定
m <- round(N/4)
####################
# 周波数の定義
freq <- (0:m)/(2*m)
####################
PSD0 <- c()
####################
for(ii in 1:N.samps){
 ####################
 # 白色ノイズの生成 
 w <- rnorm(N,0,sqrt(sig2))
 ####################
 # 空の変数を事前に準備
 # 初期値をy[1]=w[1]とする
 y[1] <- w[1]
 for(n in 2:N){
  y[n] <- a*y[n-1]+w[n]
 }
 ######################
 # 自己共分散の推定 (sample autocovariance)
# a.cov <- rep(N,(m+1))/(N:(N-m))*acf(y,lag.max=m,type="covariance",plot=FALSE)$acf[,,1]

 a.cov <- acf(y,lag.max=m,type="covariance",plot=FALSE)$acf[,,1]

 PSD <- numeric(m+1)
 v.acov <- c(a.cov[1],2*a.cov[2:m],a.cov[m+1]) 
 for(i in 1:(m+1)){
  v.cos <- cos((i-1)*(0:m)*pi/m)
  PSD0[i] <- v.acov %*% v.cos 
 }
 ####################
 # 平滑化（これがないと，スペクトルがマイナスになることがあります）
 PSD[2:m] <- PSD0[2:m]*0.5+0.25*PSD0[1:(m-1)]+0.25*PSD0[3:(m+1)]
 PSD[1] <- (PSD0[1]+PSD0[2])/2
 PSD[m+1] <- (PSD0[m]+PSD0[m+1])/2
 ######################
 if(ii == 1){
  PSD.samps <- data.frame(PSD)
 }else{
  PSD.samps <- cbind(PSD.samps,data.frame(PSD))
 }
}
f <- freq #[freq>=0 & freq<=0.5]
Spec <- rowMeans(PSD.samps)

###############
plot(f[-1],Spec[-1],"l",col=4,log="xy",main="log-log plot",xlab="f",xaxt="n",yaxt="n",xaxs="i",ylab="Spectrum")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),add=TRUE,col=2,lwd=2,lty=2,n=1000)