【Rで時系列解析】スペクトルウインドーを使ったパワースペクトルの平滑化：Rの"spectrum"での"spans"オプションの意味

今回は，離散フーリエ変換でえられるギザギザなパワースペクトルを，滑らかにする「平滑化」についてです．いろいろ書きたいことはありますが，まずは，Rでお世話になることが多い"spectrum"というコマンドのオプション"spans"について説明します．今回の説明は，私が数値実験をして確認したことに基づいていますので，間違いがあるかもしれません．他人を簡単に信じないでください．

1. パワースペクトルの平滑化

　一般的な平滑化の説明をしておきます．離散フーリエ変換を使って計算されたパワースペクトル $S(f_k)$ の平滑化は，重み $\{w_j\}$ ( $j=-m, \cdots, 0, \cdots, m$ )を使って，

　 $\displaystyle \hat{S}(f_k) = \sum_{j=-m}^{m} w_{j}\, S(f_{k-j})$

と表されます．

　移動平均で平滑化する場合は，

　 $\displaystyle w_{j} = \frac{1}{2m+1}\quad$ ( $-m \le j \le m$ )

です (下図)．時系列の移動平均と同じように，パワースペクトル $S(f_k)$ が平滑化されます．

2. "spans"の使用例

　Rの"spectrum"コマンドを使ったことがない人もいるかもしれませんし，使ったことはあっても，"spans"オプションを指定したことがない人もいるかもしれませんので，まずは，数値実験の結果をお見せします．時系列は2次自己回帰過程 ( $a_1 = 1.6$ , $a_2 = -0.9$ )で生成しました．時系列のベクトルデータをx.simとすれば，使ったコマンドは，

spectrum(x.sim, ...)

です．"..."の部分はオプションコマンドが入ります．例えば，グラフを描かない場合は，

spectrum(x.sim, plot=FALSE)

とします．

　"spans"を使った結果は下の図です．平滑化していない結果 (左上)と比べて，平滑化すると，解析的結果 (赤破線)と推定結果 (青実線)の一致が良くなっています．

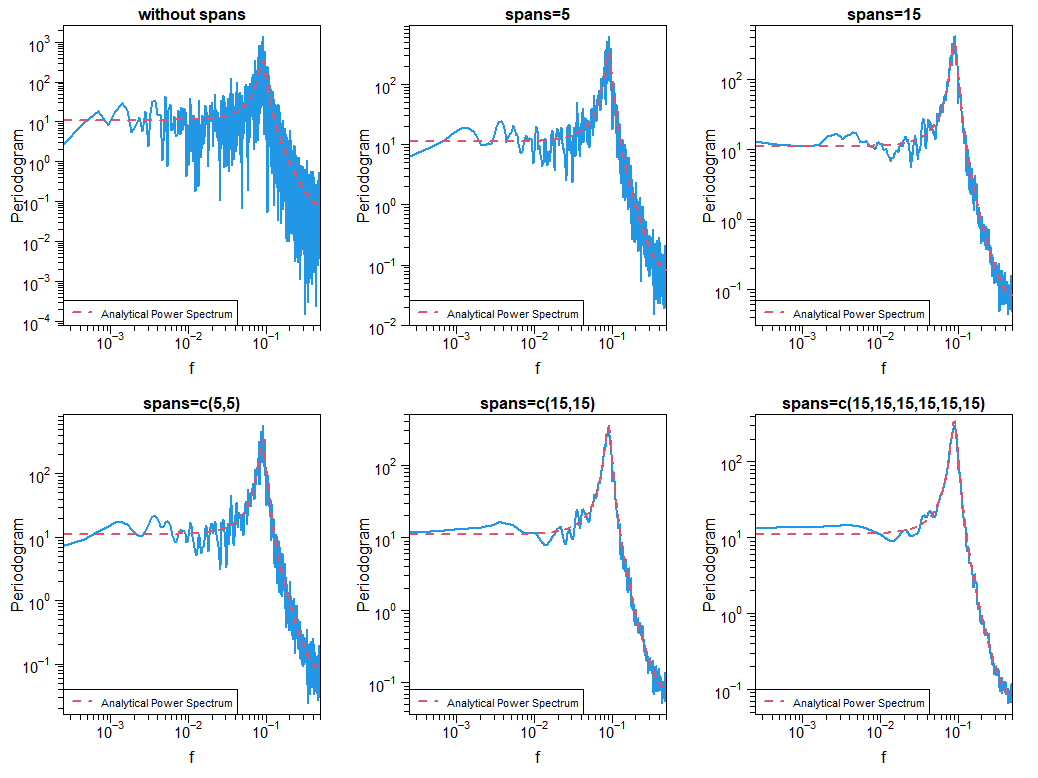
　指定した"spans"は，各図の上のタイトル部分に書いてあります．図の左上から順番に，対応するRのコマンドを書けば，

tmp <- spectrum(x.sim, plot=FALSE)
tmp <- spectrum(x.sim, spans=5, plot=FALSE)
tmp <- spectrum(x.sim, spans=15, plot=FALSE)
tmp <- spectrum(x.sim, spans=c(5,5), plot=FALSE)
tmp <- spectrum(x.sim, spans=c(15,15), plot=FALSE)
tmp <- spectrum(x.sim, spans=c(15,15,15,15,15,15), plot=FALSE)

です．この場合，"tmp$freq"に周波数，"tmp$spec"に推定されたスペクトル密度が入っています．

　"spans"を指定すれば，平滑化できていることは見て取れます．でも，これで何をやっているの？ "spans=c(15,15,15,15,15,15)"って，マニュアルの使用例に載っていないし，ふざけてんのか？と感じる人も多いと思います．

3. Rのマニュアルの説明を見ると

　"spectrum"を実行した場合，デフォルトで実際の動いているのは"spec.pgram"のようです．Rコンソールで

?spec.pgram

を実行すれば，マニュアルを見ることができます．そこでは，"spans"のオプションについて，
　
　「ピリオドグラムを平滑化するために使用される修正ダニエルスムーザ (modified Daniell smoothers)の幅を与える奇数を並べたベクトル．」

と書いてあります．つまり，"spans=c(3,5,15,9,7,11)"のように，奇数のベクトルを指定しろということです．

　以下で，"spans=c(...)"の意味を読み解いていきます．

4. 修正ダニエルスムーザ (modified Daniell smoothers)とは

　まず，修正版ではない，元の「ダニエルスムーザ」は，単なる移動平均フィルタ (スムーザ)です．つまり，最初に説明した例と全く同じです．

【ダニエルスムーザ】
　平均をとる全幅 (点数)が $L=2 m + 1$ のとき，
　 $\displaystyle w_{j} = \left\{ \begin{array}{ll} \displaystyle \frac{1}{2m+1} \quad& (-m \le j \le m)\\ \displaystyle 0 \quad & ({\rm otherwise}) \end{array} \right.$

　ダニエルスムーザと修正ダニエルスムーザの違いは，両端の点にあります (下図)．

　上図の右のように修正ダニエルスムーザでは，両端の重みが，中央部の重みの半分になります．つまり，式で書くと以下です．

【修正ダニエルスムーザ】
　平均をとる全幅 (点数)が $L=2 m + 1$ のとき，
　 $\displaystyle w_{j} = \left\{ \begin{array}{ll} \displaystyle \frac{0.5}{2 m} \quad & (j = - m)\\ \displaystyle \frac{1}{2 m} \quad& (-(m-1) \le j \le m-1) \\ \displaystyle \frac{0.5}{2 m} \quad& ( j = m ) \\ \displaystyle 0 \quad& ({\rm otherwise}) \end{array} \right.$

　何で端の重みのみ半分にするのか，私には理由は分かりません．想像で考えると， $m=1$ のときなど，幅が小さいときに，中央の点の重みを大きくできるので，元の構造を壊さないように軽～くスムージングするには修正版が良いかもしれません． $m$ が大きくなると，ダニエルも修正ダニエルも，結果はほぼ同じだと思います．

5. "spans"で指定する値の意味

　"spectrum"コマンドのオプション"spans"では，修正ダニエルスムーザの長さ $L$ を指定しています ( $L=2 m + 1$ )．以下のように，

spectrum( ... , spans=L, ... )

1つの値 $L$ だけ指定すれば，上で説明した修正ダニエルで平滑化されます．

　さらに，以下のように，

spectrum( ... , spans=c(L, M, N), ... )

ベクトルで指定すると，3回修正ダニエルスムーザがかけられます．つまり，1回目は長さ $L$ の修正ダニエルスムーザ，2回目は長さ $M$ の修正ダニエルスムーザ，3回目は長さ $N$ の修正ダニエルスムーザになります．

　このように，複数回修正ダニエルスムーザをかけると，重み $\displaystyle w_{j}$ のバランスを変えられます．まだ，「確率密度関数の特性関数」と「畳込み定理」について説明していないので，ここからの説明は理解できない人がいるかもしれません．ポイントは，何回も何回も修正ダニエルスムーザ (あるいは，もとのダニエルスムーザ)をかけていくと，重み $\displaystyle w_{j}$ が正規分布に近づきます．２回だと三角形に近い重み分布になります．

　"spans"の設定により，平滑化をする重み $\displaystyle \{w_{j}\}$ がどのようになるのかを見るRスクリプトを載せておきます．

spans <- "c(5,5,5)"
w0 <- kernel("modified.daniell",m=eval(parse(text = spans)))$coef
w <- c(rev(w0[-1]),w0)
m <- (length(w)-1)/2
j <- (-m):(m)
w.max <- max(w)
plot(j,w,ylim=c(0,w.max*1.1),pch=16,col=2,las=1,yaxs="i",main=paste("spans =",spans))
arrows(j, 0, j, w, col =2,length=0,lwd=2)

最初の行の

spans <- "c(5,5,5)"

の部分に，"spans=c(...)"で指定する右辺のベクトルを書いてください．

　この記事も参考にしてください．
chaos-kiyono.hatenablog.com

おまけ

# 時系列の長さ (時系列は奇数長になります)
N <- 2^12
# 奇数に変換
N <- round(N/2)*2+1
# 半分
M <- (N-1)/2
#########################
# モデルの自己共分散関数を与える
# 例：AR(2)過程の自己共分散関数
AR2.model <- function(n,a1,a2,sig2){
 Cov <- c()
 Cov[1] <- sig2*(1-a2)/(1-a1^2-a2-a1^2*a2-a2^2+a2^3)
 Cov[2] <- Cov[1]*a1/(1-a2)
 for(k in 3:(n+1)){
  Cov[k] <- a1*Cov[k-1] + a2*Cov[k-2]
 }
 return(Cov)
}
# パラメタの設定
a1 <- 1.6
a2 <- -0.9
sig2 <- 1
# 【注意】[-M,M]区間ではなく，[0,2M-1]にしている
acov.model <- c(AR2.model(M,a1,a2,sig2),rev(AR2.model(M,a1,a2,sig2)[-1]))
lag <- c(0:M,-(M:1))
#########################
# 自己共分散関数のフーリエ変換
fft.model <- fft(acov.model)
PSD.model <- Re(fft.model)
f <- c((0:M)/N,-(M:1)/(N))
#########################
# 白色ノイズの生成
WN <- rnorm(N)
#　ホワイトノイズのフーリエ変換
fft.WN <- fft(WN)
#########################
# サンプル時系列の生成
fft.sim <-  sqrt(PSD.model)*fft.WN
x.sim <- Re(fft(fft.sim,inverse=TRUE))/N
#########################
# 結果の描画
par(mfrow=c(2,3),cex.main=1.5,cex.axis=1.4,cex.lab=1.7,las=1,mar=c(5,5,2,2))
########################################################################
# PSDの推定
# spansなし
tmp <- spectrum(x.sim,plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("without spans"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
########################################################################
# PSDの推定
# spans=5
tmp <- spectrum(x.sim,spans=5,plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("spans=5"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
########################################################################
# PSDの推定
# spans=15
tmp <- spectrum(x.sim,spans=15,plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("spans=15"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
########################################################################
# PSDの推定
# spans=c(5,5)
tmp <- spectrum(x.sim,spans=c(5,5),plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("spans=c(5,5)"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
########################################################################
# PSDの推定
# spans=c(15,15)
tmp <- spectrum(x.sim,spans=c(15,15),plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("spans=c(15,15)"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
########################################################################
# PSDの推定
# spans=c(15,15,15,15,15,15)
tmp <- spectrum(x.sim,spans=c(15,15,15,15,15,15),plot="false")
freq <- tmp$freq
psd <- tmp$spec
#
plot(freq[freq > 0],psd[freq > 0],"l",log="xy",col=4,pch=16,xlim=c(f[2],0.5),xaxs="i",xlab="f",ylab="Periodogram",main=paste("spans=c(15,15,15,15,15,15)"),lwd=2,xaxt="n",yaxt="n")
lines(f[f > 0],PSD.model[f > 0],col=2,lwd=2,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
legend("bottomleft", legend=c("Analytical Power Spectrum"), col=c(2), lty=c(2),lwd=c(2))
##########################################################