【Rで時系列解析】1/fノイズの自己共分散 (自己相関)関数は対数関数で，べきじゃない

今回は，1/fノイズ (ピンクノイズ)の自己共分散 (自己相関)関数についての話です．つまり，

　 $\displaystyle S(f) \propto \frac{1}{f}$

となる時系列の自己共分散 (自己相関)関数は，

　 $C(k) \propto - \log k$

ということを説明します．解析的に導出しようかと思いましたが，この論文
doi.org
の流れをなぞるだけになるのでやめます．途中の計算が分からなければ質問して下さい．この論文では，以下の記事で紹介したような特別なモデルを仮定して，自己共分散 (自己相関)関数を導出しています．
chaos-kiyono.hatenablog.com
　しかし，どんなモデルでも，1/fノイズ (ピンクノイズ)であれば，自己共分散 (自己相関)関数は，いつでも対数関数的に減衰します (私の経験談です)．

　ということで数値実験で確認です．前回の記事で1/fノイズ (ピンクノイズ)のサンプル時系列の生成方法を説明しました．
chaos-kiyono.hatenablog.com

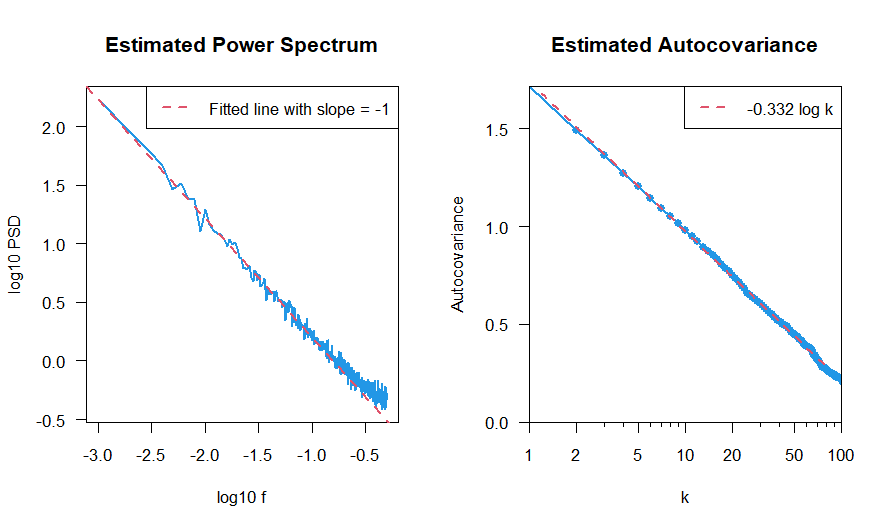
　いろんな方法で，サンプル時系列を生成して，どの場合も，自己共分散 (自己相関)関数が $C(k) \propto - \log k$ になることを確認します．以下では，100本のサンプル時系列を生成して，パワースペクトルと自己共分散 (自己相関)関数を推定しました．青が実際の推定結果，赤は線がフィットの結果です．パワースペクトルは，両対数をとったプロット，自己共分散 (自己相関)は，横軸のみ対数目盛の片対数プロットになっていることに注意してください．自己共分散 (自己相関)関数が，片対数プロットで直線になるということは，対数関数になっているということです．

1. パワースペクトルを与えて時系列を生成した場合

　パワースペクトルが，

　 $\displaystyle S(f) = \frac{1}{f_0 + |f|}$
　
に従う時系列を生成して，自己共分散 (自己相関)関数を推定します． $f_0$ は，非常に小さい定数です．

2. ARFIMA(0, d, 0)の掟破りのd = 0.5で時系列を生成した場合

　次の式で， $m = 0.5$ として，時系列を生成します．
　 $\begin{eqnarray} y[n] &=& \sum_{j=0}^{\infty} \frac{ \Gamma (j+m)}{\Gamma (j+1) \Gamma (m)} w[n-j] \end{eqnarray}$ $\displaystyle$
ここで， $\{w[n]\}$ は，平均0，分散 $\sigma^2$ の白色ノイズです．

3. 中点変位法で生成する方法

　２点の中点位置に，平均0，分散 $\sigma^2$ の正規乱数を足していけば，1/fノイズ (ピンクノイズ)になります．

まとめ

　1/fノイズ (ピンクノイズ)を含む広い意味で「長時間相関」という表現を使っている論文で，「自己共分散 (自己相関)関数がべき的に減衰する」とか，「べき的自己共分散 (自己相関)関数」という記述をときどき目にします．今回，数値実験で確かめたように，1/fノイズ (ピンクノイズ)の自己共分散 (自己相関)関数は対数関数的に減衰するので，それは間違いです．とはいえ，本質はそこにあるのではなく，1/fノイズ (ピンクノイズ)の自己共分散 (自己相関)関数は，定常の意味では存在しないことを認識しておくことが重要です．

　だって，1/fノイズ (ピンクノイズ)の自己共分散 (自己相関)関数の見て，不思議な感じがしませんでしたか？というのは，自己共分散 (自己相関)関数が対数関数的に減衰する場合，ラグが増加していくと，自己共分散 (自己相関)関数は，いつか0に到達するからです．1/fノイズ (ピンクノイズ)の記憶 (相関)は有限なの？と思えることが不思議なのです．今回は，有限長の時系列から無理矢理，自己共分散 (自己相関)関数を計算してみた，ということです．

　このブログで私は，数学的な理想の世界の時系列解析ではなく，現実世界にある有限の長さの時系列解析の基礎を整理したいと考えています．ちょくちょく間違いを犯すと思いますが，恐れずに，従来の教科書の枠組みをはみ出していきたいと思います．

おまけ：使用したRスクリプト

　「1. パワースペクトルを与えて時系列を生成した場合」の数値実験．

# 時系列の長さ
N <- 1001
# 奇数に変換
N <- round(N/2)*2+1
# 半分
M <- (N-1)/2
#########################
# 1/fゆらぎの近似パワースペクトル
# f0は，高周波数側で無相関になるカットオフ周波数
PSD1.model <- function(f,f0){
 return(1/(f0 + abs(f)))
}
#########################
# 両側パワースペクトル
f0 <- 1/(10*N)
f <- c((0:M)/N,-(M:1)/(N))
PSD.model <- PSD1.model(f,f0)
##############################################
# サンプル時系列の総数
N.ens <- 100
PSD <- c()
ACOR <- c() 
for(i in 1:N.ens){
#########################
# 白色ノイズの生成
WN <- rnorm(N)
#　ホワイトノイズのフーリエ変換
fft.WN <- fft(WN)
#########################
fft.sim <-  sqrt(PSD.model)*fft.WN
#########################
x.sim <- Re(fft(fft.sim,inverse=TRUE))/N
###############################################
# 以下は検証用プロット
################
TMP <- acf(x.sim,plot=FALSE,type="covariance",lag.max=round(N/4))
Ac.y <- TMP$acf[,,1]
X <- fft(x.sim)
S.y <- abs(X)^2/N
 if(i == 1){
  PSD <- S.y
  ACOR <- Ac.y
 }else{
  PSD <- PSD+S.y
  ACOR <- ACOR + Ac.y
 }
}
PSD <- PSD/N.ens
ACOR <- ACOR/N.ens
################################################
# グラフ用パラメタ設定
par(mfrow=c(1,2),pty="m",cex=1.1,las=1)
#
fit <- lm(log10(PSD[f>0 & f < 0.1])~log10(f[f>0 & f < 0.1]))
plot(log10(f[f>0]),log10(PSD[f>0]),col=4,pch=16,"l",lwd=2,xlab="log10 f",ylab="log10 PSD",main="Estimated Power Spectrum")
abline(fit,lty=2,col=2,lwd=2)
legend("topright", legend=c(paste("Fitted line with slope =",format(fit$coefficients[[2]],digit=2))), col=c(2), lty=c(2),lwd=c(2))
#################################################
k.lag <- 1:length(ACOR)-1
plot(k.lag[k.lag>0],ACOR[k.lag>0],pch=16,col=4,"o",log="x",lwd=2,xlim=c(1,N/10),ylim=c(0,ACOR[2]),xaxs="i",yaxs="i",xlab="k",ylab="Autocovariance",main="Estimated Autocovariance")
axis(1,at=10^(0:5)%x%(1:9),label=FALSE,tck=-0.015)
fit <- lm(ACOR[k.lag>0 & k.lag < N/10]~log(k.lag[k.lag>0 & k.lag < N/10]))
curve(fit$coefficients[[1]] + fit$coefficients[[2]]*log(x),add=TRUE,lwd=2,col=2,lty=2)
legend("topright", legend=c(paste(format(fit$coefficients[[2]],digit=3),"log k")), col=c(2), lty=c(2),lwd=c(2))

　「2. ARFIMA(0, d, 0)の掟破りのd = 0.5で時系列を生成した場合」の数値実験．

# 時系列の長さ
N <- 1001
# 奇数に変換
N <- round(N/2)*2+1
# 半分
M <- (N-1)/2
#########################
# パラメタの設定
m <- 0.5
sig2 <- 1
sig <- sqrt(sig2)
j.max <- N
j <- 0:j.max
coef <- exp(lgamma(j+m)-lgamma(j+1)-lgamma(m))
#########################
# サンプル時系列の総数
N.ens <- 100
PSD <- c()
ACOR <- c() 
for(i in 1:N.ens){
 #########################
 # 白色ノイズの生成
 w <- rnorm(N+j.max,0,sig)
 # 移動平均の計算
 x.sim <- c()
 for(k in 1:N){
  x.sim[k] <- w[(k+j.max):k] %*% coef
 }
###############################################
# 以下は検証用プロット
################
TMP <- acf(x.sim,plot=FALSE,type="covariance",lag.max=round(N/4))
Ac.y <- TMP$acf[,,1]
X <- fft(x.sim)
S.y <- abs(X)^2/N
 if(i == 1){
  PSD <- S.y
  ACOR <- Ac.y
 }else{
  PSD <- PSD+S.y
  ACOR <- ACOR + Ac.y
 }
}
PSD <- PSD/N.ens
f <- c((0:N)/N)
ACOR <- ACOR/N.ens
################################################
# グラフ用パラメタ設定
par(mfrow=c(1,2),pty="m",cex=1.1,las=1)
#
fit <- lm(log10(PSD[f>0 & f < 0.1])~log10(f[f>0 & f < 0.1]))
plot(log10(f[f>0 & f <= 1/2]),log10(PSD[f>0 & f <= 1/2]),col=4,pch=16,"l",lwd=2,xlab="log10 f",ylab="log10 PSD",main="Estimated Power Spectrum")
abline(fit,lty=2,col=2,lwd=2)
legend("topright", legend=c(paste("Fitted line with slope =",format(fit$coefficients[[2]],digit=2))), col=c(2), lty=c(2),lwd=c(2))
#################################################
k.lag <- 1:length(ACOR)-1
plot(k.lag[k.lag>0],ACOR[k.lag>0],pch=16,col=4,"o",log="x",lwd=2,xlim=c(1,N/10),ylim=c(0,ACOR[2]),xaxs="i",yaxs="i",xlab="k",ylab="Autocovariance",main="Estimated Autocovariance")
axis(1,at=10^(0:5)%x%(1:9),label=FALSE,tck=-0.015)
fit <- lm(ACOR[k.lag>0 & k.lag < N/10]~log(k.lag[k.lag>0 & k.lag < N/10]))
curve(fit$coefficients[[1]] + fit$coefficients[[2]]*log(x),add=TRUE,lwd=2,col=2,lty=2)
legend("topright", legend=c(paste(format(fit$coefficients[[2]],digit=3),"log k")), col=c(2), lty=c(2),lwd=c(2))

　「3. 中点変位法で生成する方法」の数値実験．

##########################
# 分割する回数 (回数を増やすと時系列が長くなります)
n.step <- 12
##########################
# サンプル時系列の総数
N.ens <- 100
##########################
PSD <- c()
ACOR <- c() 
for(i in 1:N.ens){
　#########################
　# 時系列の生成
　################
　# 最初の２点
　x <- c(0,1)
　y <- c(0,0) 
　################
　k <- 2
　for(j in 1:n.step){
　 h <- (1/2)^j
　 x.tmp <- x[1:k]
　 y.tmp <- y[1:k]
　 x[(1:(k-1))*2] <- (x.tmp[1:(k-1)]+x.tmp[2:k])/2
　 y[(1:(k-1))*2] <- (y.tmp[1:(k-1)]+y.tmp[2:k])/2+rnorm(k-1)
　 x[(1:k)*2-1] <- x.tmp
　 y[(1:k)*2-1] <- y.tmp
　 k <- k + (k-1)
　}
 x.sim <- y
 N <- length(x.sim)
###############################################
# 以下は検証用プロット
################
TMP <- acf(x.sim,plot=FALSE,type="covariance",lag.max=round(N/4))
Ac.y <- TMP$acf[,,1]
X <- fft(x.sim)
S.y <- abs(X)^2/N
 if(i == 1){
  PSD <- S.y
  ACOR <- Ac.y
 }else{
  PSD <- PSD+S.y
  ACOR <- ACOR + Ac.y
 }
}
PSD <- PSD/N.ens
f <- c((0:N)/N)
ACOR <- ACOR/N.ens
################################################
# グラフ用パラメタ設定
par(mfrow=c(1,2),pty="m",cex=1.1,las=1)
#
fit <- lm(log10(PSD[f>0 & f < 0.1])~log10(f[f>0 & f < 0.1]))
plot(log10(f[f>0 & f <= 1/2]),log10(PSD[f>0 & f <= 1/2]),col=4,pch=16,"l",lwd=2,xlab="log10 f",ylab="log10 PSD",main="Estimated Power Spectrum")
abline(fit,lty=2,col=2,lwd=2)
legend("topright", legend=c(paste("Fitted line with slope =",format(fit$coefficients[[2]],digit=2))), col=c(2), lty=c(2),lwd=c(2))
#################################################
k.lag <- 1:length(ACOR)-1
plot(k.lag[k.lag>0],ACOR[k.lag>0],pch=16,col=4,"o",log="x",lwd=2,xlim=c(1,N/10),ylim=c(0,ACOR[2]),xaxs="i",yaxs="i",xlab="k",ylab="Autocovariance",main="Estimated Autocovariance")
axis(1,at=10^(0:5)%x%(1:9),label=FALSE,tck=-0.015)
fit <- lm(ACOR[k.lag>0 & k.lag < N/10]~log(k.lag[k.lag>0 & k.lag < N/10]))
curve(fit$coefficients[[1]] + fit$coefficients[[2]]*log(x),add=TRUE,lwd=2,col=2,lty=2)
legend("topright", legend=c(paste(format(fit$coefficients[[2]],digit=3),"log k")), col=c(2), lty=c(2),lwd=c(2))