【Ｒで時系列解析】Detrending moving average algorithm (DMA)を使った長時間相関スケーリング解析

今回はDetrending moving average algorithm (DMA)をＲでやってみます．DMAの参考文献はこれです（ダウンロードできない人が多いと思います．オープンアクセスの良い論文を見つけられませんでした）：
Detrending Moving Average algorithm: a brief review | IEEE Conference Publication | IEEE Xplore

ここでは，signalパッケージのSavitzky-Golayフィルタを使って，積分時系列の移動平均を計算し，この移動平均をトレンドとして除きます．

まずは，解析する時系列の準備です．これまで何度かお世話になっているlongmemoパッケージを使います．分析したい時系列がある場合は，このRスクリプトは無視して，xに時系列をベクトルとして格納してください．

# パッケージのインストールが必要な場合は以下を実行
# install.packages("longmemo")
# パッケージのロード
require(longmemo)
###################################
# パラメタの設定：ハースト指数(0 < H < 1)
H <- 0.6
# 時系列の長さ
n <- 2^10
####################################
# 非整数ガウスノイズの生成 
x <- simFGN0(n,H)

以下は，DMAの説明用のグラフ作成も一緒にやるRスクリプトです．

#
# xを時系列ベクトルとする
#
N <- length(x)
###############################
# Savitzky-Golay フィルタにsignalパッケージを使用 
# install.packages("signal")
require(signal)
###############################
#　平均0化
x <- x - mean(x)
# 積分
y <- cumsum(x)
###############################
# 作図用のパラメタ
par(mfrow=c(3,2))
par(pty="m",cex=1.1,las=1,cex.lab=1.2)
par(mar=c(5,4,2,2))
# 解析対象の時系列
plot(1:N,x,"l",col=4,xaxs="i",xlab="i",ylab="x[i]",lwd=2,main="Original time series")
plot(1:N,y,"l",col=4,xaxs="i",xlab="i",ylab="y[i]",lwd=2,main="Integrated series")
###############################
# scalesの設定
scale.min <- 4
scale.max <- N/4
scale <- unique(round(10^seq(log10(scale.min),log10(scale.max),0.05)/2)*2+1)
n.scale <- length(scale)
# プロットする3つのスケールの指定
p.scale <- c(3,round(3+(n.scale-3)/2),n.scale-2)
###############################
F2 <- c()
for(i in 1:n.scale){
 F2[i] <- 0
 i.edge <- (scale[i]-1)/2
 y.sg <- sgolayfilt(y,p=0,n=scale[i],m=0,ts=1)
 if(is.element(i, p.scale)){
  plot(1:N,y,"l",col=4,xaxs="i",lwd=2,xlab="i",ylab="y[i]",main=paste("scale =",scale[i]))
  lines((i.edge+1):(N-i.edge),y.sg[(i.edge+1):(N-i.edge)],col=2,lty=2,lwd=2)
 }
 F2[i] <- mean((y[(i.edge+1):(N-i.edge)]-y.sg[(i.edge+1):(N-i.edge)])^2)
}
###############################
# 結果のプロット
par(pty="s")
fit <- lm(log10(F2)/2~log10(scale))
plot(log10(scale),log10(F2)/2,xlab="log10 n",ylab="log10 F(n)",main=paste("slope =",format(fit$coefficients[[2]],digit=2)))
points(log10(scale[p.scale]),log10(F2[p.scale])/2,pch=16,col=2)
abline(fit,lty=2,col=2,lwd=2)

このスクリプトを実行すると，下のような図が出力されます．

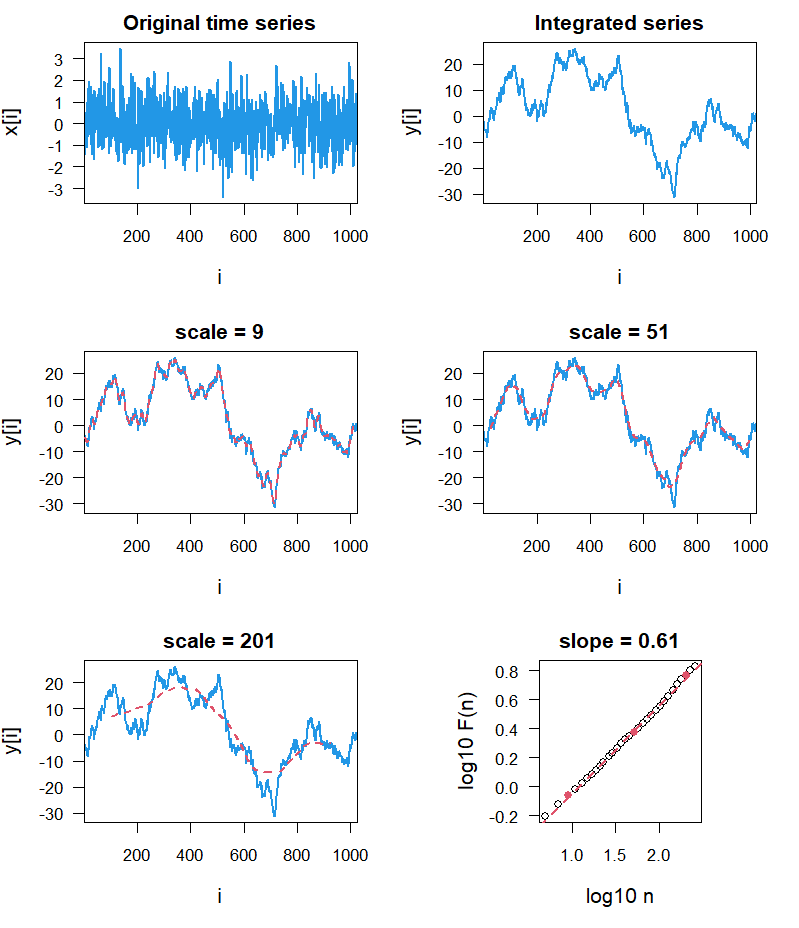
上の図では，左上に解析する時系列x，その右が積分時系列，下の時系列は，各スケールで区分的に直線（赤実線）を当てはめた結果，右下がスケーリング解析（ $\log_{10} n$ に対する $\log_{10} F(n)$ ）の結果です．

実際の時系列解析では，こんなに図は必要ないので，スクリプトはこんな感じになります．

#
# xを時系列ベクトルとする
#
N <- length(x)
###############################
# Savitzky-Golay フィルタにsignalパッケージを使用 
# install.packages("signal")
require(signal)
###############################
#　平均0化
x <- x - mean(x)
# 積分
y <- cumsum(x)
###############################
# scalesの設定
scale.min <- 4
scale.max <- N/4
scale <- unique(round(10^seq(log10(scale.min),log10(scale.max),0.05)/2)*2+1)
n.scale <- length(scale)
###############################
F2 <- c()
for(i in 1:n.scale){
 F2[i] <- 0
 i.edge <- (scale[i]-1)/2
 y.sg <- sgolayfilt(y,p=0,n=scale[i],m=0,ts=1)
 F2[i] <- mean((y[(i.edge+1):(N-i.edge)]-y.sg[(i.edge+1):(N-i.edge)])^2)
}
###############################
# 結果のプロット
par(pty="s")
fit <- lm(log10(F2)/2~log10(scale))
plot(log10(scale),log10(F2)/2,xlab="log10 n",ylab="log10 F(n)",main=paste("slope =",format(fit$coefficients[[2]],digit=2)))
points(log10(scale[p.scale]),log10(F2[p.scale])/2,pch=16,col=2)
abline(fit,lty=2,col=2,lwd=2)