【確率変数】変数変換したら確率密度関数はどうなるか - ケィオスの時系列解析メモランダム

確率変数を変数変換する話です．

変数変換した後の確率密度関数
線形変換の例
指数変換の例

変数変換した後の確率密度関数

　ここでは，確率変数 $X$ が，確率密度関数 $f_{X}(x)$ に従うとします．このとき，単調関数 (単調増加か，単調減少する関数) $g(x)$ を使って，確率変数 $Y$ が

　 $Y = g(X)$

で与えられるとします． $Y$ が従う確率密度関数 $f_{Y}(y)$ を求めたいな，というのがここでの問題です．

　変数変換しても，確率は保存しないといけません．つまり，確率密度関数の対応する部分の面積が一致して，

　 $\begin{eqnarray} P\left(a < X < b \right) &=& P\left( g(a) < Y < g(b) \right) \\ \int_{x = a}^{x=b}\!f_{X}(x)\, dx &=& \int_{y=g(a)}^{y=g(b)}\!f_{Y}(y)\, dy \end{eqnarray}$

となる必要があります．

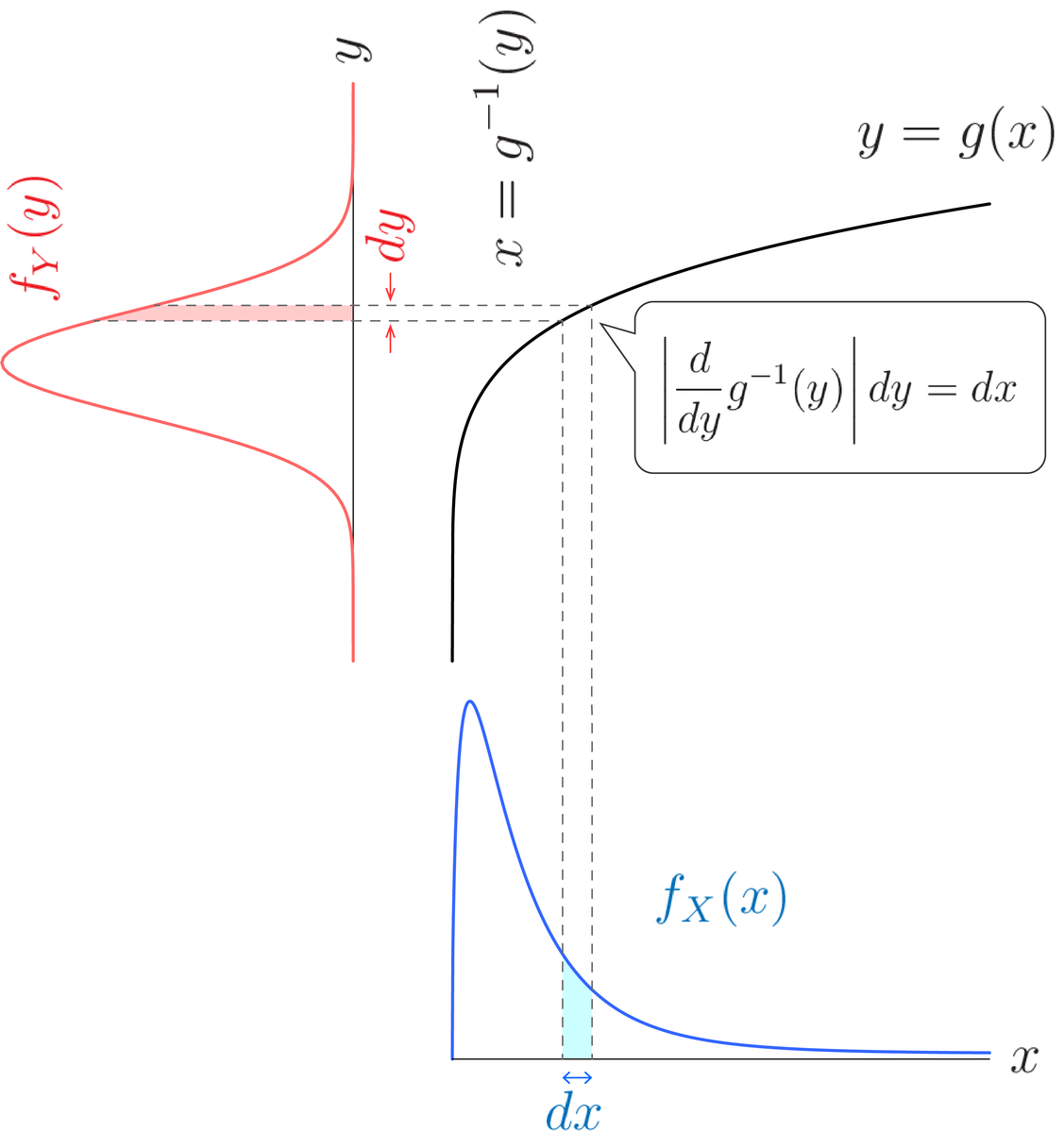
　左辺を， $y = g(x)$ と置換した積分を考えると，

　 $\begin{eqnarray} \displaystyle \int_{x = a}^{x=b}\!f_{X}(x)\, dx = \int_{y=g(a)}^{y=g(b)}\!f_{X}\left(g^{-1}(y) \right) \frac{d \left(g^{-1}(y)\right)}{dy} \, dy \end{eqnarray}$

とできそうです． $\frac{d \left(g^{-1}(y) \right)}{dy}$ は，対応する微小面積の倍率を表しています．確率は常に0以上で，マイナスになってはダメなので，プラスマイナスは無視することにすれば，

　 $\begin{eqnarray} \displaystyle \int_{x = a}^{x=b}\!f_{X}(x)\, dx = \int_{y=g(a)}^{y=g(b)}\!f_{X}\left(g(y) \right) \left| \frac{d \left(g^{-1}(y)\right)}{dy} \right| \, dy \end{eqnarray}$

となります (一般の多重積分も，向きの違いのプラスマイナスを無視するので，ヤコビアンには絶対値がついてます)．

　ということで，確率 (面積)の保存を表す

　 $\begin{eqnarray} \int_{x = a}^{x=b}\!f_{X}(x)\, dx &=& \int_{y=g(a)}^{y=g(b)}\!f_{Y}(y)\, dy \end{eqnarray}$

と対応する部分を比べると，

　 $\begin{eqnarray} f_{Y}(y) &=& f_{X}(g^{-1}(y))\, \left| \frac{d \left(g^{-1}(y) \right)}{dy} \right| \end{eqnarray}$

となることがわかります．

　あらためて書くと，

確率変数 $X$ が確率密度関数 $f_{X}(x)$ に従うとき，単調関数を使って $Y = g(X)$ と変数変換すると， $Y$ の確率密度関数は，

　 $\begin{eqnarray} f_{Y}(y) &=& f_{X}(g^{-1}(y))\, \left| \frac{d \left(g^{-1}(y) \right)}{dy} \right| \end{eqnarray}$

ということです．

線形変換の例

　 $X$ が標準正規分布 (平均0，分散1の正規分布)に従うとします．このとき， $\sigma$ ， $\mu$ を定数として，

　 $\begin{eqnarray} f_{X}(x) &=& \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \end{eqnarray}$

です．

　 $\sigma$ ， $\mu$ を定数として，確率変数 $Y$ が

　 $Y = \sigma X+\mu$

で与えられる場合を考えます．

　 $\displaystyle X = \frac{Y-\mu}{\sigma}$ なので， $\displaystyle g^{-1}(y) = \frac{y-\mu}{\sigma}$ です．

　したがって，確率変数 $Y$ が従う確率密度関数は，

　 $\begin{eqnarray} f_{Y}(y) &=& f_{X}(g^{-1}(y))\, \left| \frac{d \left(g^{-1}(y) \right)}{dy} \right| \\ &=& f_{X}(g^{-1}(y))\, \frac{1}{\sigma} \\ &=& \frac{1}{\sqrt{2 \pi}} e^{-\frac{\left( \frac{y-\mu}{\sigma} \right)^2}{2}} \, \frac{1}{\sigma} \\ &=& \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(y-\mu \right)^{\,2}}{2 \sigma^2}} \end{eqnarray}$

となり，正規分布の式になります．

指数変換の例

　 $X$ が正規分布に従うとします．このとき， $\sigma$ ， $\mu$ を定数として，

　 $\begin{eqnarray} f_{X}(x) &=& \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(y-\mu \right)^{\,2}}{2 \sigma^2}} \end{eqnarray}$

です．

　確率変数 $Y$ が

　 $Y = \exp X$

で与えられる場合を考えます．

　 $\displaystyle X = \log Y$ なので， $\displaystyle g^{-1}(y) = \log y$ です．

　したがって，確率変数 $Y$ が従う確率密度関数は，

　 $\begin{eqnarray} f_{Y}(y) &=& f_{X}(g^{-1}(y))\, \left| \frac{d \left(g^{-1}(y) \right)}{dy} \right| \\ &=& f_{X}(g^{-1}(y))\, \frac{1}{y} \\ &=& \frac{1}{\sqrt{2 \pi} \sigma y} e^{-\frac{\left(\log y-\mu \right)^{\,2}}{2 \sigma^2}} \end{eqnarray}$

となり，対数正規分布の式になります．