【時系列解析】２次自己回帰過程のサンプル時系列から自己共分散関数とパワースペクトルを推定

本日のセミナーの課題は，２次自己回帰過程

　 $y [n] = a_1 y [n-1] + a_2 y [n-2] + w[n$ ]

のサンプル時系列から自己共分散関数とパワースペクトルを推定することです． $w[n$ ]は，平均0，分散 $\sigma^2$ の白色ノイズです．とりあえず， $a_1 = 0.9 \sqrt{3}$ ， $a_2 = -0.81$ でやってみて，他のパラメタでも調べてみてください．

これまでの知識を使えば簡単に実行できると思います．追加の課題として，白色ノイズ $w[n$ ]の部分を，単位インパルス

　 $u[n] = \left\{\begin{array}{ll} 1 & (n=0) \\ 0 & (n \neq 0)\end{array} \right.$

に置き換えた場合の振舞も数値的に調べてみてください．インパルスをいれるタイミングは0でなくても構いません。例えば，初期値をy[1] = 0，y[2] = 0として，ｗ[n]を{0, 0, 1, 0, 0, 0, 0, 0, 0, 0,... ,0}にしてください．

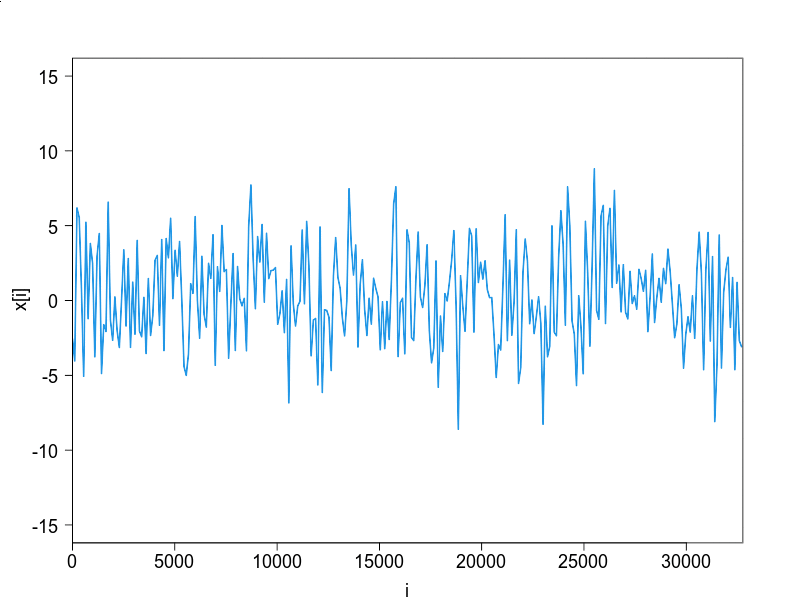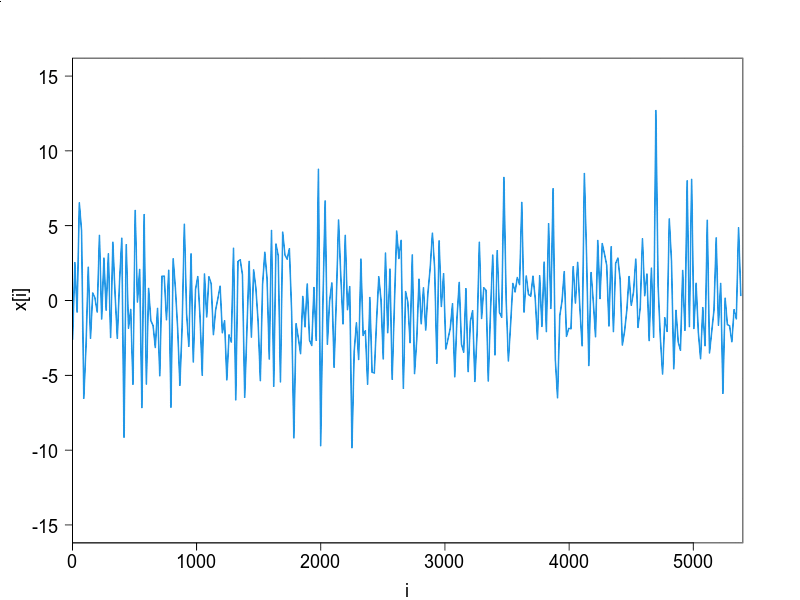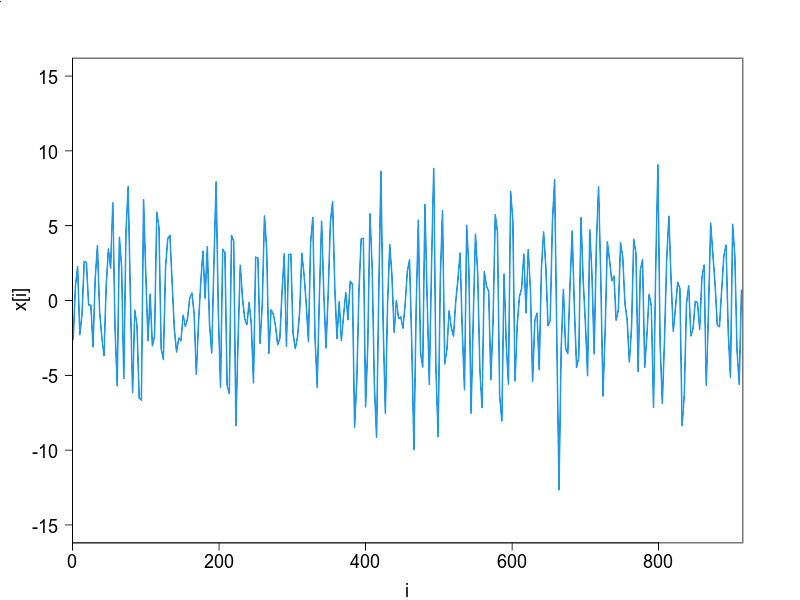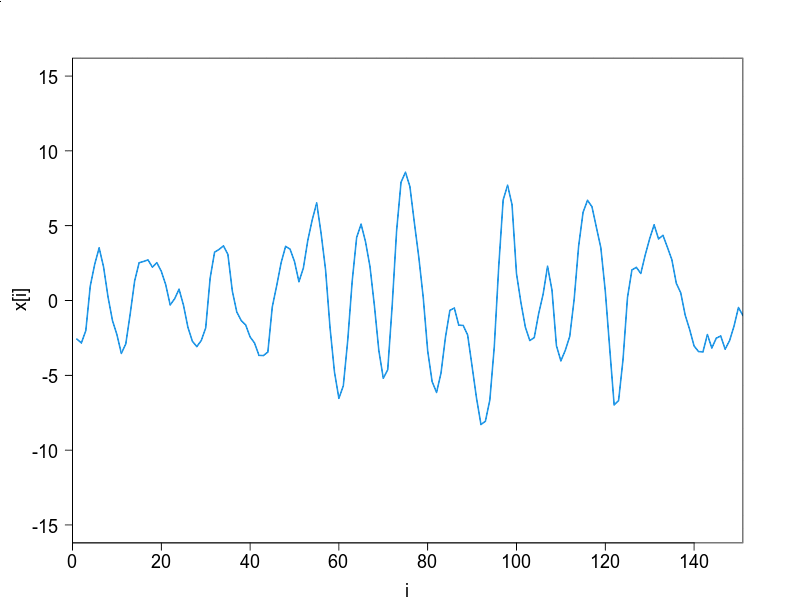
課題の解答例

ということで，Rを使って， $a_1 = 0.9 \sqrt{3}$ ， $a_2 = -0.81$ ，分散1の白色ノイズ $w[n$ ]で，パワースペクトルと自己共分散関数を推定し，解析的な結果と比較します．
a1とa2がモデルのパラメタで，Nが時系列の長さ，N.sampsがサンプルの数です．自分で値を変更して，振舞をみてください．

# 2次自己回帰過程 (2nd-order autoregressive process) 
# y[n] = a1 y[n-1] + a2 y[n-2] + w[n]
# w[n]: white noise with zero mean and variance sig^2
####################
# パラメタ (parameter)
a1 <- 0.9*sqrt(3)
a2 <- -0.81
# w[n]の標準偏差sig^2
sig2 <- 1
# 時系列の長さ
N <- 2^13
####
y <- c()
####################
# 平均をとるサンプル時系列数
N.samps <- 2^6
####################
# 最大ラグの決定
m <- N-1
####################
# 周波数の定義
freq <- (0:m)/(2*m)
####################
PSD0 <- c()
####################
for(ii in 1:N.samps){
 ####################
 # 空の変数を事前に準備
 # 初期値をy[1]=w[1]とする
　# 過渡状態を少しまわす
 w <- rnorm(20,0,sqrt(sig2))
 y[1] <- w[1]
 y[2] <- w[2]
 for(n in 3:20){
  y[n] <- a1*y[n-1]+a2*y[n-2]+w[n]
 }
 #　ここが本番
 ####################
 # 白色ノイズの生成 
 w <- rnorm(N,0,sqrt(sig2))
 y[1] <- y[19]
 y[2] <- y[20]
 for(n in 3:N){
  y[n] <- a1*y[n-1]+a2*y[n-2]+w[n]
 }
 ######################
 # 自己共分散の推定 (sample autocovariance)
 a.cov <- acf(y,lag.max=m,type="covariance",plot=FALSE)$acf[,,1]
 # fftでフーリエ・コサイン変換
 PSD0 <- Re(fft(c(a.cov,rev(a.cov[-1]))))
 ####################
 # 平滑化
 PSD <- numeric(m+1)
 PSD[2:m] <- PSD0[2:m]*0.5+0.25*PSD0[1:(m-1)]+0.25*PSD0[3:(m+1)]
 PSD[1] <- (PSD0[1]+PSD0[2])/2
 PSD[m+1] <- (PSD0[m]+PSD0[m+1])/2
 ######################
 if(ii == 1){
  PSD.samps <- data.frame(PSD)
  AutoCov.samps <- data.frame(a.cov)
 }else{
  PSD.samps <- cbind(PSD.samps,data.frame(PSD))
  AutoCov.samps <- cbind(AutoCov.samps,data.frame(a.cov))
 }
}
f <- freq 
Spec <- rowMeans(PSD.samps)
AutoCov <- rowMeans(AutoCov.samps)
#################
# 図を描く
par(mfrow=c(1,3))
#################
# パワースペクトル（横軸のみ対数スケール）
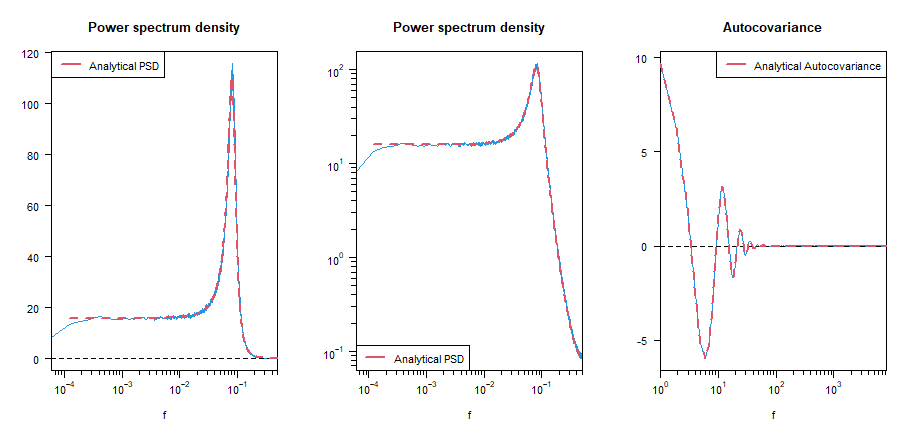
plot(f[-1],Spec[-1],"l",col=4,log="x",main="Power spectrum density",xlab="f",xaxt="n",xaxs="i",ylab="",las=1)
abline(h=0,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a1*(1-a2)*cos(2*pi*x)-2*a2*cos(4*pi*x)+a1^2+a2^2),add=TRUE,col=2,lwd=2,lty=2,n=1000,xlim=c(1/N,1/2))
legend("topleft", legend=c("Analytical PSD"), col=c(2), lty=c(1),lwd=c(2))
#######
# パワースペクトル（両対数スケール）
plot(f[-1],Spec[-1],"l",col=4,log="xy",main="Power spectrum density",xlab="f",xaxt="n",yaxt="n",xaxs="i",ylab="")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算したパワースペクトル
curve(sig2/(1-2*a1*(1-a2)*cos(2*pi*x)-2*a2*cos(4*pi*x)+a1^2+a2^2),add=TRUE,col=2,lwd=2,lty=2,n=1000,xlim=c(1/N,1/2))
legend("bottomleft", legend=c("Analytical PSD"), col=c(2), lty=c(1),lwd=c(2))
###########################################
# 自己共分散関数（横軸のみ対数スケール）
plot(1:m,AutoCov[-1],"l",log="x",col=4,main="Autocovariance",xlab="f",xaxt="n",xaxs="i",ylab="",las=1)
abline(h=0,lty=2)
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########
# 解析的に計算した自己共分散関数
acov <- c()
acov[1] <- sig2/((1-a2)^2-a1^2)*(1-a2)/(1+a2)
acov[2] <- a1/(1-a2)*acov[1]
for(i in 3:(m+1)){
 acov[i] <- a1*acov[i-1]+a2*acov[i-2]
}
lines(1:m,acov[-1],col=2,lwd=2,lty=2)
legend("topright", legend=c("Analytical Autocovariance"), col=c(2), lty=c(1),lwd=c(2))

このスクリプトを実行すれば，下の図が描かれます．

Rスクリプトの実行例．ただし，平均をとるサンプル数を増してあります．青がサンプル時系列からの推定，赤破線が解析的な結果です．

教科書の式(3.6)は，情報が抜けていて，それだけでは自己共分散関数 $C(k)$ は計算できません．たぶん，正しいものは，
$C(0) = \frac{(1-a_2) \sigma^2}{(1+a_2) \left[ (1-a_2)^2-a_1^2 \right]}$
$C(1) = \frac{a_1}{1-a_2} C(0)$
$C(k) = a_1 C(k-1) + a_2 C(k-2)$
です．来週までに，導いておいてください．

おまけ

単位インパルスを上記の過程に入れると，何が起こるか？というのが追加の課題でした．2次の自己回帰過程（特性方程式が複素数解を持つ場合）が，2階の線形微分方程式の減衰振動に対応することを感じてください．1次自己回帰過程は，1階の線形微分方程式の振舞や，過減衰（振動せずに0に漸近）に対応しています（この数値実験もしてみてください）．

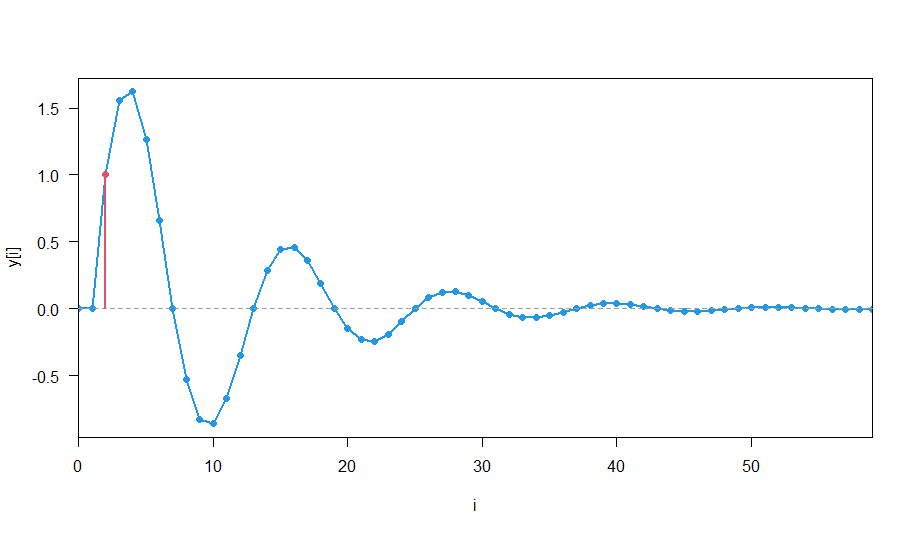
2次自己回帰過程の単位インパルスに対する応答．赤が単位インパルスが入った箇所です．

# 2次自己回帰過程 (2nd-order autoregressive process) 
# y[n] = a1 y[n-1] + a2 y[n-2] + w[n]
####################
# パラメタ (parameter)
a1 <- 0.9*sqrt(3)
a2 <- -0.81
# 
y[1] <- 0
y[2] <- 0
# wに{0,0,1,0,0,....,0}を代入
w <- numeric(N) # N個0が代入される
w[3] <- 1 #3番目に1を代入
###
for(n in 3:N){
  y[n] <- a1*y[n-1]+a2*y[n-2] + w[n]
}
par(mfrow=c(1,1))
plot(1:N-1,y,"o",pch=16,col=4,xaxs="i",las=1,xlab="i",ylab="y[i]",lwd=2)
abline(h=0,col=8,lty=2)
lines(c(2,2),c(0,1),col=2,lwd=2)
points(c(2),c(1),pch=16,col=2)