北川 源四郎先生の本「Rによる 時系列モデリング入門」(33 ページ)では,
「ラグが大きくなるとき自己共分散関数
が急激に減衰し」
という条件が,パワースペクトル
の定義を与える部分に書いてあります (以下では,を
と書きます).何で? この条件「自己共分散関数
が急激に減衰」の部分を読み飛ばしてはいけないというのが今回のお話です.
Wikipediaのウィーナー=ヒンチンの定理 (Wiener–Khinchin theorem)の説明
ja.wikipedia.org
にはそんなこと書いてないけど,と思うかもしれません.
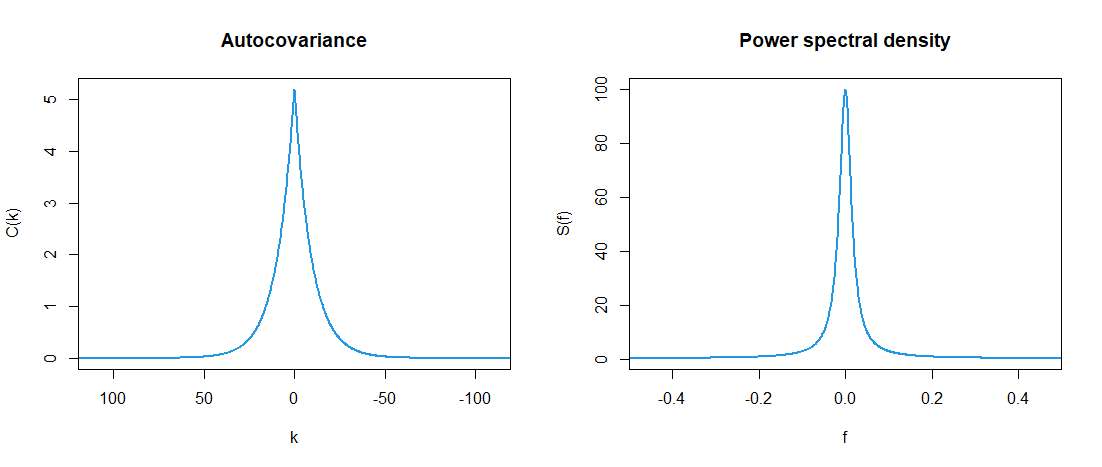
自己共分散とパワースペクトルの関係
時系列の自己共分散関数を,
とします.ここでは,で期待値を表しています.このとき,次のような有限の長さ
の時系列のパワースペクトルの推定量の期待値
を計算してみます.ここでは,時系列のフーリエ変換を使ってパワースペクトルを計算すると (パワースペクトルの定義は複数あります (関連記事1)),
となります (ちょっと自信がありませんので自分で確かめてください).途中で,
の公式を使いました.これは,離散の単位インパルス (ディラックじゃありません)
のフーリエ変換が
になることの逆変換です.フーリエ変換と逆フーリエ変換には1対1の関係がありますので片方が分かれば,逆も言えます.
となったので,さらに,とすれば,
になりそうですが,本当にそうでしょうか.問題は,
の部分です.がすごーく大きいときは,
がそこそこ大きくても,
と近似するには無理があります.
このような無理をしないために,がすごーく大きくなる前に,
の増加にともない急速に
となってくれる必要があるのです.つまり,
「ラグが大きくなるとき自己共分散関数
が急激に減衰し」
の条件が必要なのです.とはいえ,なぜ,自己共分散関数のフーリエ変換でパワースペクトルを定義しているのかについては,私は十分に理解できていません.弱定常過程の前提ありきなのかなと想像しています.どなたか,詳しい方に教えていただきたいです.
練習問題 (すごく重要だと思います.お気に入りの問題です)
次の確率過程ではない例
の自己共分散関数 (減衰せずに振動し続けとる (下図参照))
を使って,パワースペクトルを計算してみてください.この自己共分散関数は,
として,無理矢理計算しました.は任意の値です.
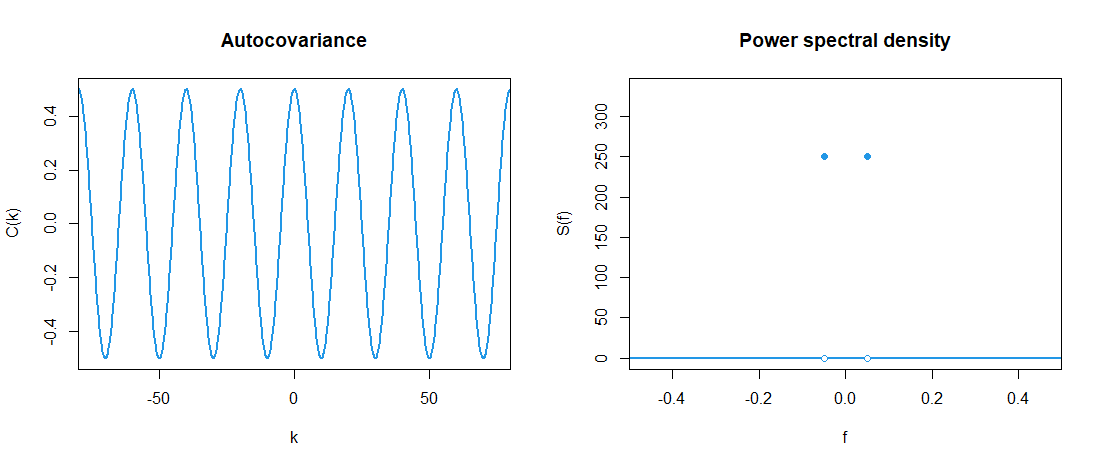
長さの時系列
のフーリエ変換を使ったパワースペクトルの計算結果 (これは,
で収束しないぞ!)は,
となります (上の図右側).「えー,なんでNがかかってんの?」と感じること,疑問に思うことが大切です.パワースペクトルというのは,正式にはパワースペクトル密度です.パワースペクトル密度の面積が,時系列の分散に一致するのでした.この場合,長方形で近似することにすれば (三角形でもいいですが),周波数の幅を使って,全面積は
となります.これは,時系列の分散と一致します (正しそうです).
ということで,上に示したパワースペクトルと,自己共分散関数
のフーリエ変換 (ウィーナー=ヒンチンの定理)を使ったパワースペクトルの計算を比較してください (発散しちゃうぞ!).
のフーリエ変換が存在しないことに気づいてください.
ちなみに,上で導いた関係式
で計算すると,
となり,上に書いたパワースペクトルと一致します.
関連記事
1. パワースペクトルの定義
chaos-kiyono.hatenablog.com
2. 1次自己回帰過程
chaos-kiyono.hatenablog.com
chaos-kiyono.hatenablog.com
chaos-kiyono.hatenablog.com
chaos-kiyono.hatenablog.com
おまけ
作図に使ったRスクリプト
sig2 <- 1 a <- 0.9 par(mfrow=c(1,2)) ######## # 解析的に計算した自己共分散関数 curve(sig2/(1-a^2)*a^abs(x),col=4,lwd=2,n=1000,xlim=c(-4*pi/log(a),4*pi/log(a)),xlab="k",ylab="C(k)",main="Autocovariance",xaxs="i") # 解析的に計算したパワースペクトル curve(sig2/(1-2*a*cos(2*pi*x)+a^2),col=4,lwd=2,n=1000,xlim=c(-1/2,1/2),xlab="f",ylab="S(f)",main="Power spectral density",xaxs="i")
k <- 50 N <- 1000 A <- 1 par(mfrow=c(1,2)) ######## # 解析的に計算した自己共分散関数 curve(1/2*cos(2*pi*k/N*x),xlim=c(-N/k*4,N/k*4),col=4,lwd=2,xlab="k",ylab="C(k)",main="Autocovariance",xaxs="i",n=1000) # 解析的に計算したパワースペクトル curve(0*x,col=4,lwd=2,n=100,xlim=c(-1/2,1/2),ylim=c(0,N/3),xlab="f",ylab="S(f)",main="Power spectral density",xaxs="i") points(c(k/N,(N-k)/N-1),c(N/4*A^2,N/4*A^2),pch=16,col=4) points(c(k/N,(N-k)/N-1),c(0,0),pch=16,col="white") points(c(k/N,(N-k)/N-1),c(0,0),pch=1,col=4)