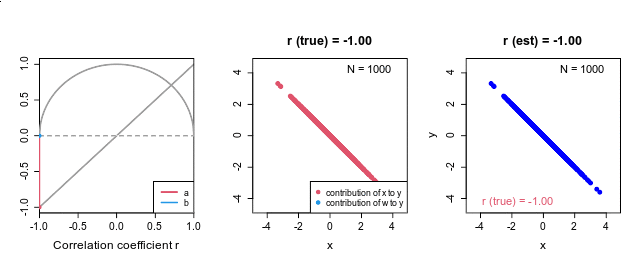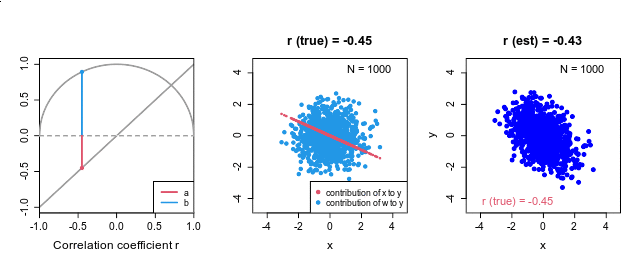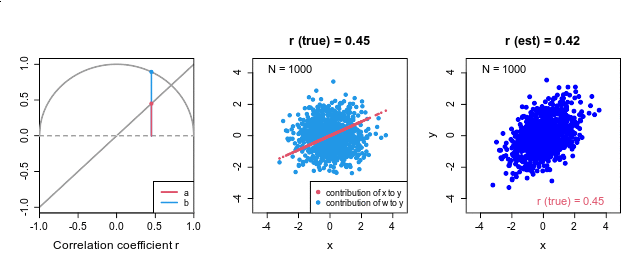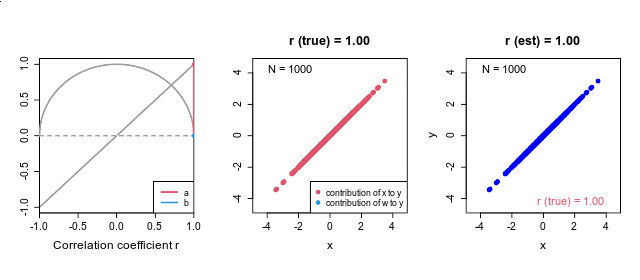
複数のデバイス で同時計測をしたとき,計測時刻のズレが発生することがあります.今回は,そのズレを相互相関を使って修正する方法について説明します.
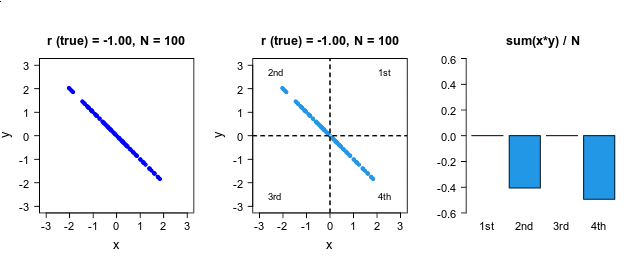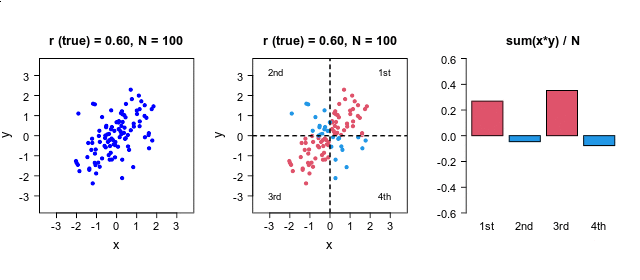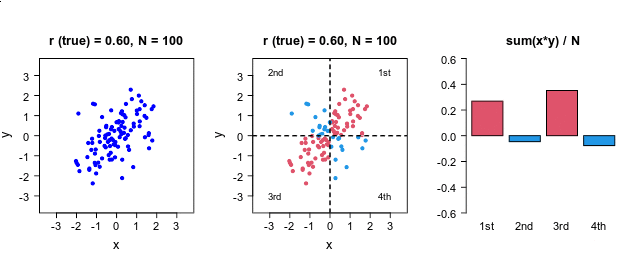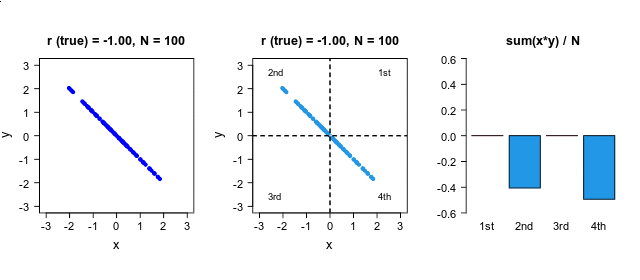
下の図では,左上のグラフのように,赤の
2本の時系列の時間のズレを推定 この時間のズレは,相互相関係数 の絶対値が最大になる時間差を推定することで評価できます.上の例では,右上の相互相関のグラフが最大になる点 (lag=38)が,推定された時間差になります.相関係数 というのは,2つの変量の直線的な関係性を評価していますので,右下の散布図のように,相互相関が最大になる点 (lag=38)で,2つの変数の値が最も45度の直線的に集まってきます.
時間差が推定できれば,
数値的に時系列を生成して,時間差を補正するスクリプト の例が以下です.
# 真のラグを設定
lag.true <- 38
# サンプル時系列を生成
N <- 1000
time <- 1:(N+lag.true)
x.base <- dnorm(time,N/2,N/5)*sin(2*pi*time/(N/3.5))^2
#
x1 <- x.base[1:N]+rnorm(N)*0.0001
x2 <- x.base[(1+lag.true):(N+lag.true)]+rnorm(N)*0.0001
time <- 1:N
######################################
par(mfrow=c(2,2),cex=1,cex.lab=1.6)
par(pty="m",mgp=c(2.2,0.5,0))
plot(time,x1,"l",col=2,xlab="i",ylab="",yaxt="n",ylim=c(-0.0005,0.003),lwd=2)
lines(time,x2,col=4,lwd=2)
legend("topright",legend=c(expression(paste(x[1],"[i]")),expression(paste(x[2],"[i]"))),col=c(2,4),lwd=c(2,2),cex=1.2)
#################
# 相互相関を使って時間を推定
xcor <- ccf(x1,x2,lag.max=round(N/4),main="",ylab="Cross-Correlation",col="skyblue")
# 相互相関係数の絶対値が最大になるラグを検出
lag.max <- xcor$lag[which.max(abs(xcor$acf))]
# 推定されたラグを破線としてプロット
abline(v=lag.max,col=6,lty=2,lwd=2)
###
plot(time,x1,"l",col=2,xlab="i",ylab="",main=paste("lag =",lag.max),yaxt="n",ylim=c(-0.0005,0.003),lwd=2)
# x2の時刻をlag.maxだけずらす
lines(time+lag.max,x2,col=4,lwd=2)
legend("topright",legend=c(expression(paste(x[1],"[i]")),expression(paste(x[2],"[i-lag]"))),col=c(2,4),lwd=c(2,2),cex=1.2)
########
# 散布図
par(pty="s",mgp=c(0.9,0,0))
if(lag.max >=0){
plot(x1[(1+lag.max):N],x2[1:(N-lag.max)],pch=16,xaxt="n",yaxt="n",xlab=expression(paste(x[1],"[i]")),ylab=expression(paste(x[2],"[i-lag]")),main=paste("lag =",lag.max),col=6)
}else{
plot(x1[1:(N+lag.max)],x2[(1-lag.max):N],pch=16,xaxt="n",yaxt="n",xlab=expression(paste(x[1],"[i]")),ylab=expression(paste(x[2],"[i-lag]")),main=paste("lag =",lag.max),col=6)
}
時刻データを補正するサンプルスクリプト が以下です.このスクリプト ではt1,t2に時刻ベクトル,x1,x2に数値データを代入しないと動きません.
# サンプリング間隔
t.samp <- 1
#####################
### 基準時系列
# 時刻
t1 <- (POSIXctの時刻)
# データ
x1 <- (時系列のベクトル)
#####################
### 時刻調整を行う時系列
# 時刻
t2 <- (POSIXctの時刻)
# データ
x2 <- (時系列のベクトル)
#####################
t.start <- max(min(t1[is.finite(x1)]),min(t2[is.finite(x2)]))
t.end <- min(max(t1[is.finite(x1)]),max(t2[is.finite(x2)]))
t.resamp <- seq(t.start,t.end,t.samp)
###
x1.tmp <- approx(t1,x1,xout=t.resamp,method="linear")$y
x2.tmp <- approx(t2,x2,xout=t.resamp,method="linear")$y
###
par(mfrow=c(1,3),cex=1,cex.lab=1.6)
plot(t.resamp,x1.tmp,"l",col=2,xlab="Original Time",ylab="")
legend("topleft",legend=c("Reference Time Series","Target Time Series"),col=c(2,4),lwd=c(1,1),cex=0.8)
lines(t.resamp,x2.tmp,col=4)
xcor <- ccf(x1.tmp,x2.tmp,lag.max=round(length(t.resamp)/4),main="",ylab="Cross-Correlation",col="skyblue")
t.lag <- xcor$lag[which.max(abs(xcor$acf))]
abline(v=t.lag,col="blue",lwd=2,lty=2)
###
plot(t.resamp,x1.tmp,"l",col=2,xlab="Corrected Time",ylab="",main=paste("Time Lag =",Lag.sec,"sec"))
Lag.sec <- t.lag*t.samp
lines(t.resamp+Lag.sec,x2.tmp,col=4)
legend("topleft",legend=c("Reference Time Series","Target Time Series"),col=c(2,4),lwd=c(1,1),cex=0.8) このスクリプト を適用した例が下の図です.
スクリプト の適用例
まとめ
私はウクライナ の研究者との共同研究を,4年くらい前から続けています.ロシア侵攻が発生した後も,ほぼ毎週,オンラインで打ち合わせをしています.しかし,2週間前から,電力不足などの問題で,ウクライナ からミーティングに接続できなくなりました.
私は東日本大震災 のときに,福島県 に住んでおり,震災後はしばらく近所の小学校に避難していました.そのとき,燃料不足で暖房が使えず,とても寒かった経験があります.寒すぎて私は一睡もできませんでした.そして,そんな寒さから逃れるために家族を,福島県 から避難させました.原発 事故よりも,寒さの方がきつかったです.
ウクライナ では多くの人が寒さに苦しんでいると思います.状況が少しでも改善することを祈っています.
が,確率密度関数
に従うとします.このとき,単調関数 (単調増加か,単調減少する関数)
を使って,確率変数
が
が従う確率密度関数
を求めたいな,というのがここでの問題です.
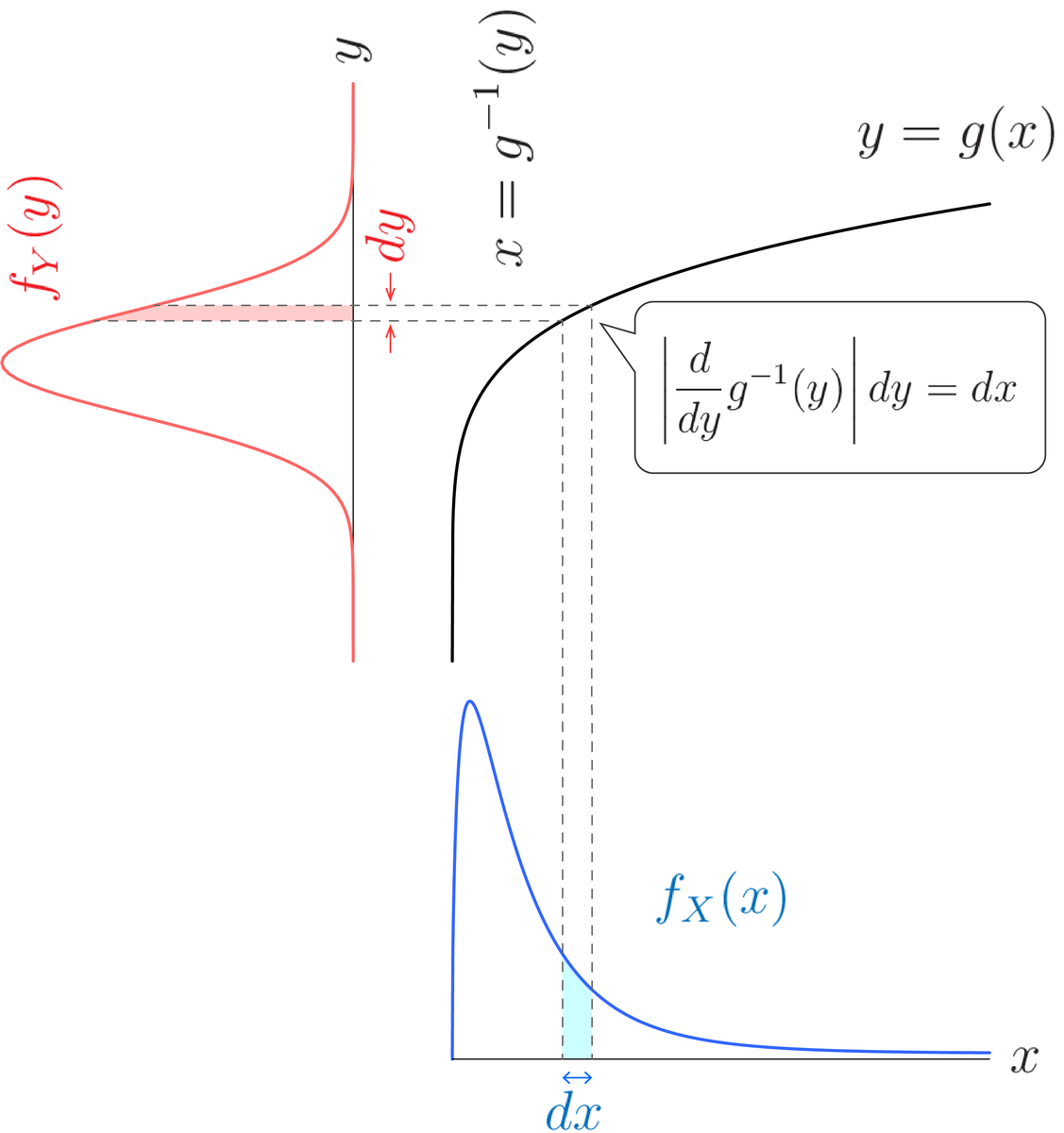
と置換した積分を考えると,
は,対応する微小面積の倍率を表しています.確率は常に0以上で,マイナスになってはダメなので,プラスマイナスは無視することにすれば,