【時系列のフラクタル解析】DMAの使い方（C言語プログラムの配布と使い方）

時系列の長時間相関解析やフラクタル解析（統計的自己アフィン性の解析）を行うのに，最近の20年間でDetrended fluctuation analysis (DFA)が使われることが多くなっています．DFAは神話化がはじまっており，その本質や欠点がきちんと理解されていないというのが私の意見です．今回は，DFAについては詳しく述べません．今回は，DFAと似た方法であるDetrending moving average (DMA) algorithmとその高次元版を使ってみようというのがテーマです．参考文献は以下です：

Yutaka Tsujimoto, Yuki Miki, Satoshi Shimatani, Ken Kiyono, "Fast algorithm for scaling analysis with higher-order detrending moving average method"，Physical Review E 93，053304 (2016)．
Anna Carbone, Ken Kiyono，"Detrending moving average algorithm: Frequency response and scaling performances"，Physical Review E 93，063309 (2016)．
Ken Kiyono，"Theory and applications of detrending-operation-based fractal-scaling analysis"， International Conference on Noise and Fluctuations (ICNF) (2017)．

DMAのC言語プログラム

C言語のプログラムを，以下のリンクからダウンロードできるようにしておきました．
https://www.dropbox.com/s/7kvxo2f63clj3q6/cDMA.zip?dl=0
zipファイルを解凍すると，以下のプログラムが含まれています．

cDMA0.c	0次の中心DMAの高速アルゴリウムのプログラム
cDMA2.c	2次の中心DMAの高速アルゴリウムのプログラム
cDMA4.c	4次の中心DMAの高速アルゴリウムのプログラム

使ってみたい人は，これらのプログラムをコンパイルして実行形式のファイルを作ってください．ここでは，実行形式のファイル名をそれぞれ，

cDMA0.exe	cDMA0.cをコンパイルしたもの
cDMA2.exe	cDMA2.cをコンパイルしたもの
cDMA4.exe	cDMA4.cをコンパイルしたもの

とします．

分析する時系列の作成

自分で分析したい時系列データがある人はそれを分析すればいいですが，ない人はパソコンで人工的に（数値的に）時系列を作って，それを分析してみてください．ここで作るデータは，フラクタル性の答え（スケーリング指数の真の値）が分かっているので，時系列解析が正しくできているか確認するのに役立ちます．時系列の生成にはRを使います．以下のスクリプトをRで実行してください．

Rスクリプトの注意点は，事前にデータをlongmemoパッケージをインストールしておくこと，時系列を保存するフォルダを事前に作って指定すること，つまり，

D:\Document\時系列解析

の場合は，バックスラッシュ("\"，日本語環境では￥マーク)を，"/"に書き直す必要がありますので，下記のRスクリプトの2行目にある

DIR <- "...... ここに各自，データを保存したいフォルダへのパスを指定 ......"

の部分を

DIR <- "D:/Document/時系列解析"

に変更する．さらに，時系列を保存するファイル名を指定したい場合は，9行目の

FN <- "sample.csv"

のsample.csvの部分を，好きに書き換えてください．

# データを出力するフォルダ
DIR <- "...... ここに各自，データを保存したいフォルダへのパスを指定 ......"
# パッケージのインストールが必要な場合は以下を実行
# install.packages("longmemo")
# パッケージのロード
require(longmemo)
####################################
# データを保存するファイル名
FN <- "sample.csv"
####################################
# パラメタの設定
# ハースト指数(0 < H < 1)
H <- 0.8
# 時系列の長さ(長くすると，計算時間が長なり，ファイルサイズがでかくなる)
n <- 2^12
####################################
# 非整数ガウスノイズの生成 
x.fGn <- simFGN0(n,H)
####################################
# 生成データの保存 
setwd(DIR)
write.table(x.fGn,FN, sep = ",", append=FALSE, quote=FALSE, col.names=FALSE,row.names=FALSE)

DMAでフラクタル解析（ここがメイン)）

いよいよDMAの使い方の説明です．準備として，解析したい時系列データを自分のパソコンに保存しておき，その時系列データがあるフォルダに，DMAのプログラムをコンパイルした"cDMA*.exe" (*=0, 2, 4)を一緒に保存してください．

解析の流れは以下です．

解析したい時系列データが保存されているフォルダ上でコマンドプロンプトを起動
cDMA*.exeを実行
解析結果を，Rとか，エクセルとか，pythonを使ってグラフ化して観察．そして，スケーリング指数を推定．

コマンドプロンプトを起動する方法は，以下の記事を参照してください．
chaos-kiyono.hatenablog.com

ここでは，分析するデータファイルを"sample.csv"と仮定します．この"sample.csv"は，ヘッダや見出し行なしで，時系列の数値が縦一列に保存されているとします．（上で説明したRの使い方が分からず，時系列データがない人は，このリンク
https://www.dropbox.com/s/q4bfp9woyr4vj6a/sample.csv?dl=0
からダウンロードしてください．）

0次DMAを使って解析するときは，コマンドプロンプトで，

cDMA0.exe samp_series.csv > result_dma0.csv

と入力してください．ここでは，分析結果を保存するファイル名を"result_dma0.csv"としました（ファイル名は各自決めてください）．結果を保存するファイルの拡張子は".csv"とすることをお勧めします．csvファイルは，デフォルトでエクセルに関連付けられているので開くとき便利です．
コマンドプロンプトの雰囲気は以下です．

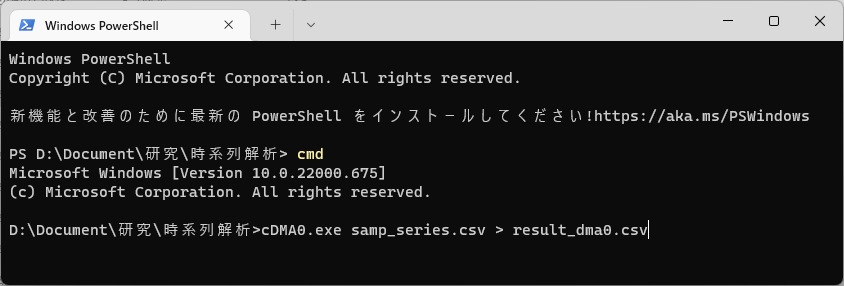
0次DMAの代わりに，2次DMAを使う場合は，cDMA0.exeの部分を"cDMA2.exe"，4次の場合は"cDMA4.exe"にしてください．

ここまでを実行したら，分析結果のファイル"result_dma0.csv"ができていることを確認してください．ファイルサイズが0でなければ，成功している可能性があります．cDMA*.exeの分析結果ファイルには，

log(補正スケール)	log(ゆらぎ関数)	log(補正なしスケール)
$log_{10} \tilde{s}$	$\log_{10} F(\tilde{s})$	$\log_{10} s$

が保存されています．解析結果をグラフにする場合は，このファイルの中身の１列目と２列目をそれぞれx軸，y軸にプロットします．

Rを使ってグラフ化し，傾きからスケーリング指数を推定するスクリプトは，こんな感じです．

# DMA結果のファイル名
FN <- "result_dma0.csv"
###########################
# データの読み込み
TMP <- read.csv(FN,header=FALSE)
###########################
# プロット
par(mfrow=c(2,1))
plot(TMP$V1,TMP$V2,pch=1,col=4,xlab="log s",ylab="log F(s)",las=1)
############################
# スケーリング領域
log.s1 <- 1.0
log.s2 <- 2.5
fit <- lm(TMP$V2[TMP$V1 >= log.s1 & TMP$V1 <= log.s2]~TMP$V1[TMP$V1 >= log.s1 & TMP$V1 <= log.s2])
b <- fit$coefficients[[1]]
a <- fit$coefficients[[2]]
abline(v=c(log.s1,log.s2),col=8,lty=2)
curve(a*x+b,add=TRUE,xlim=c(log.s1,log.s2),lty=2,lwd=2,col=2)
text((log.s1+log.s2)/2,a*log.s1+b,paste("slope =",format(a,digits=3)),col=2)
############################
# 局所スロープ（隣接する２点の傾き）
slope.loc <- diff(TMP$V2)/diff(TMP$V1)
plot(TMP$V1[-1],slope.loc,pch=1,col=4,xlab="log s",ylab="local slope",ylim=c(0,1.5),las=1)
abline(v=c(log.s1,log.s2),col=8,lty=2)
curve(a+0*x,add=TRUE,xlim=c(log.s1,log.s2),lty=2,lwd=2,col=2)

このスクリプトを実行すると，以下のような図が作成されます．上段が $\log_{10} F(s)$ に対する $\log_{10} s$ のグラフです．下段は隣接する２点の傾きです．