【時系列解析】自己回帰過程のパラメタとパワースペクトルの関係

今回は，一般に $m$ 次自己回帰過程

　 $y[n] = a_1 y[n-1] + a_2 y[n-2] + \cdots + a_m y[n-m] + w[n]$

のパラメタ $\{a_1, a_2, \cdots, a_m\}$ と， $w[n]$ の分散 $\sigma^2$ (平均は０とします)がわかったときに，そのパワースペクトルを導きます．というか，パワースペクトルをとりあえず式で書きます．

　今回は，パワースペクトルのパラメトリック推定を理解するための準備になってます．

　これまでの２次自己回帰過程の話で，すでに方法はわかったと思います．まず，基本事項 (使う道具)の確認です．

基本事項の確認

1. ラグオペレータ $L$ を，時系列 $\{x[i]\}$ に作用させると，

$\displaystyle L x [i] = x[i-1]$ ，　 $\displaystyle L^m x [i] = x[i-m]$

となります．つまり， $L$ が1つかかるごとに，時間が１戻ります．

2. 時系列 $\{x[i]\}$ のフーリエ変換を $X(f)$ とします．時間の世界でのラグオペレータ $L$ をフーリエ変換すると， $e^{{\bf i } 2 \pi f}$ になります．つまり，

$\displaystyle L x [i]$ をフーリエ変換すると， $\displaystyle e^{{\bf i} 2 \pi f} X(f)$

となります．フーリエ変換すると， $L$ が $e^{{\bf i} 2 \pi f}$ に変わると覚えてください．

3. 時系列 $\{x[i]\}$ のパワースペクトルの推定量 $S_x(f)$ は，長さ $N$ の時系列 $\{x[i]\}$ のフーリエ変換を $X(f_k)$ (ここで， $f_k = k/N$ )として，

$\displaystyle S_x(f_k) = \frac{|X(f_k)|^2}{N}$

です．

パワースペクトルの導出

　以下の自己回帰過程

　 $y[n] = a_1 y[n-1] + a_2 y[n-2] + \cdots + a_m y[n-m] + w[n]$

を，ラグオペレータ $L$ を使って表すと，

　 $\begin{eqnarray} y[n] &=& a_1 L y[n] + a_2 L^2 y[n] + \cdots + a_m L^m y[n] + w[n] \\ y[n] - \left(a_1 L y[n] + \cdots + a_m L^m y[n] \right) &=& w[n] \\ \left(1 - a_1 L + \cdots + a_m L^m \right) y[n] &=& w[n] \\ y[n] &=& \frac{1}{1 - a_1 L + a_2 L^2 + \cdots + a_m L^m} w[n] \\ \end{eqnarray}$

　ここから，両辺のフーリエ変換をして，両辺の絶対値をとって，両辺を２乗して，両辺を $N$ でわると.....
左辺は，

　 $y[n]$ が， $Y(f_k)$ になって， $|Y(f_k)|$ になって， $|Y(f_k)| ^2$ になって， $\displaystyle \frac{|Y(f_k)|^2}{N}$ になるから，

最後は， $y[n]$ のパワースペクトル $S_y(f_k)$ になります．

左辺は， $w[n]$ のパワースペクトル $\sigma^2$ になります． $L$ は $\displaystyle e^{{\bf i} 2 \pi f}$ になります．

　ということで，

$\displaystyle S_y (f_k) = \frac{\sigma^2}{\left|1 - a_1 e^{{\bf i} 2 \pi f} + a_2 e^{{\bf i} 4 \pi f} + \cdots + a_m e^{{\bf i} 2 \pi f m} \right|^2}$

です．

　こんなこと，どの時系列解析の教科書にも書いてあるので，つまらないですが，ここからは， $\{a_1, a_2, \cdots, a_m\}$ と， $w[n]$ の分散 $\sigma^2$ が与えられたときのパワースペクトルをRで描いてみます．ポイントは，

　 $\{a_1, a_2, \cdots, a_m\}$ と $\sigma^2$ が決まるとパワースペクトルが計算できる

ということです．

下のスクリプトで，

a <- c(2.373596,-2.528090,1.404494)

の部分の数値や長さを変えていろいろと実験してみてください (すいません，この例は不安定で，良くない係数でした)．

# 自己回帰過程のパラメタを与える
# a <- c(a_1,a_2,...,a_m)とします
a <- c(2.373596,-2.528090,1.404494)
# 白色ノイズの分散
sig2 <- 1
####################################
m <- length(a)
# 周波数の設定　（length.outで点数を指定）
f <- seq(0,1/2,length.out=100)
n.f <- length(f)
#　パワースペクトルの計算
Sf <- c()
for(k in 1:n.f){
 Sf[k] <- 1/Re((c(1,-a) %*% exp(2*pi*f[k]*(0:m)*1i))*(c(1,-a) %*% exp(-2*pi*f[k]*(0:m)*1i)))
}
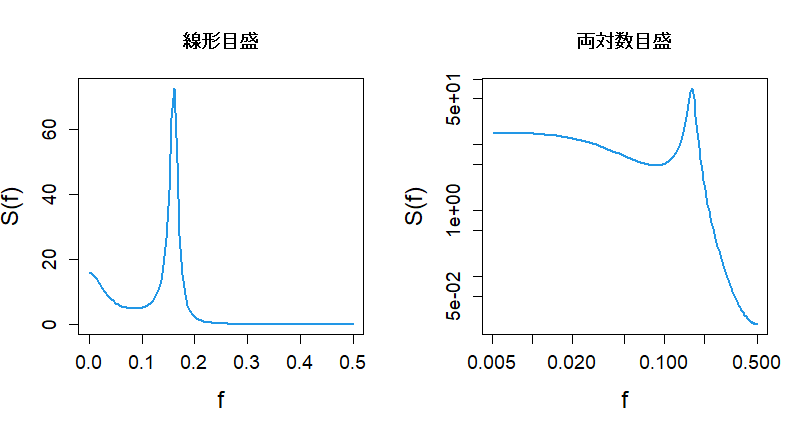
# パワースペクトルのプロット
par(mfrow=c(1,2))
plot(f,Sf,"l",col=4,lwd=2,xlab="f",ylab="S(f)",main="線形目盛")
plot(f[f>0],Sf[f>0],"l",log="xy",col=4,lwd=2,xlab="f",ylab="S(f)",main="両対数目盛")