今回は,Autoregressive fractionally integrated moving average process (ARFIMA)への導入の手前です.ARFIMAの日本語訳は,私が訳せば「自己回帰非整数積分移動平均過程」,インターネット検索でよく見る訳は「自己回帰実数和分移動平均過程」です.MA (moving average: 移動平均)過程も,ARMA (autoregressive moving average: 自己回帰移動平均)も,ARIMA (カタカナ読み「アリマ」)も,これまで全く説明していませんが,長時間相関過程の話へつなげたいので,一気に飛ばして,ARFIMA (アルフィマ,アルフィーマ)の中のARFIMA(0, d, 0)過程への導入の一歩手前の話をします.つまり,ARFIMAは,話に登場しません.
押さえておきたいポイントは,「m階差分・m階積分 (和分)のラグオペレータ (バックシフト演算子)を使った表現」と「m階差分過程・m階積分 (和分)過程のパワースペクトル」です.
基本事項の確認
以前と同じ説明です.知ってる人は飛ばしてください.
1. ラグオペレータを,時系列
に作用させると,
となります.つまり,が1つかかるごとに,時間が1戻ります.
2. 時系列のフーリエ変換を
とします.時間の世界でのラグオペレータ
をフーリエ変換すると,
になります.つまり,
となります.フーリエ変換すると,が
に変わると覚えてください.
3. 時系列のパワースペクトルの推定量
は,長さ
の時系列
のフーリエ変換を
(ここで,
)として,
です.
ラグオペレータとパワースペクトルの話は,以下の記事を参考にしてください.
m階差分・m階積分 (和分)のラグオペレータ を使った表現
を使った表現
ここでは,
となることを説明します.
まずは,1階ずつ段を進みます.の1階差分は,
です.の2階差分を
と書けば,
です.ラグオペレータを使えば,1階差分は,
2階差分は,
となります.これを繰り返せば,階差分は,
となります.
の2階積分 (和分)を
と書けば,
です.ちょっと式を書き換えてラグオペレータを使えば,1階積分 (和分)は,
2階積分 (和分)は,
となります.これを繰り返せば,階積分 (和分)は,
となります.
m階差分過程・m階積分 (和分)過程のパワースペクトル
上でとした時系列を,平均0,分散
の白色ノイズとします.ここでは,
となることを説明します.積分過程は,非定常 (時系列が発散)なので,自己共分散 (自己相関)関数のフーリエ変換として定義されるパワースペクトルは存在しません.そんなことは気にせず,有限長時系列から計算した,パワースペクトルもどきをとしていることに注意してください.
上の結果は,基本事項の2と3を使うだけです.説明が簡単すぎで,すいません.
重要なのは,m階差分過程・m階積分 (和分)過程のパワースペクトルの構造です.
下の図のように,パワースペクトルの両対数プロットには直線的な構造が現れます.
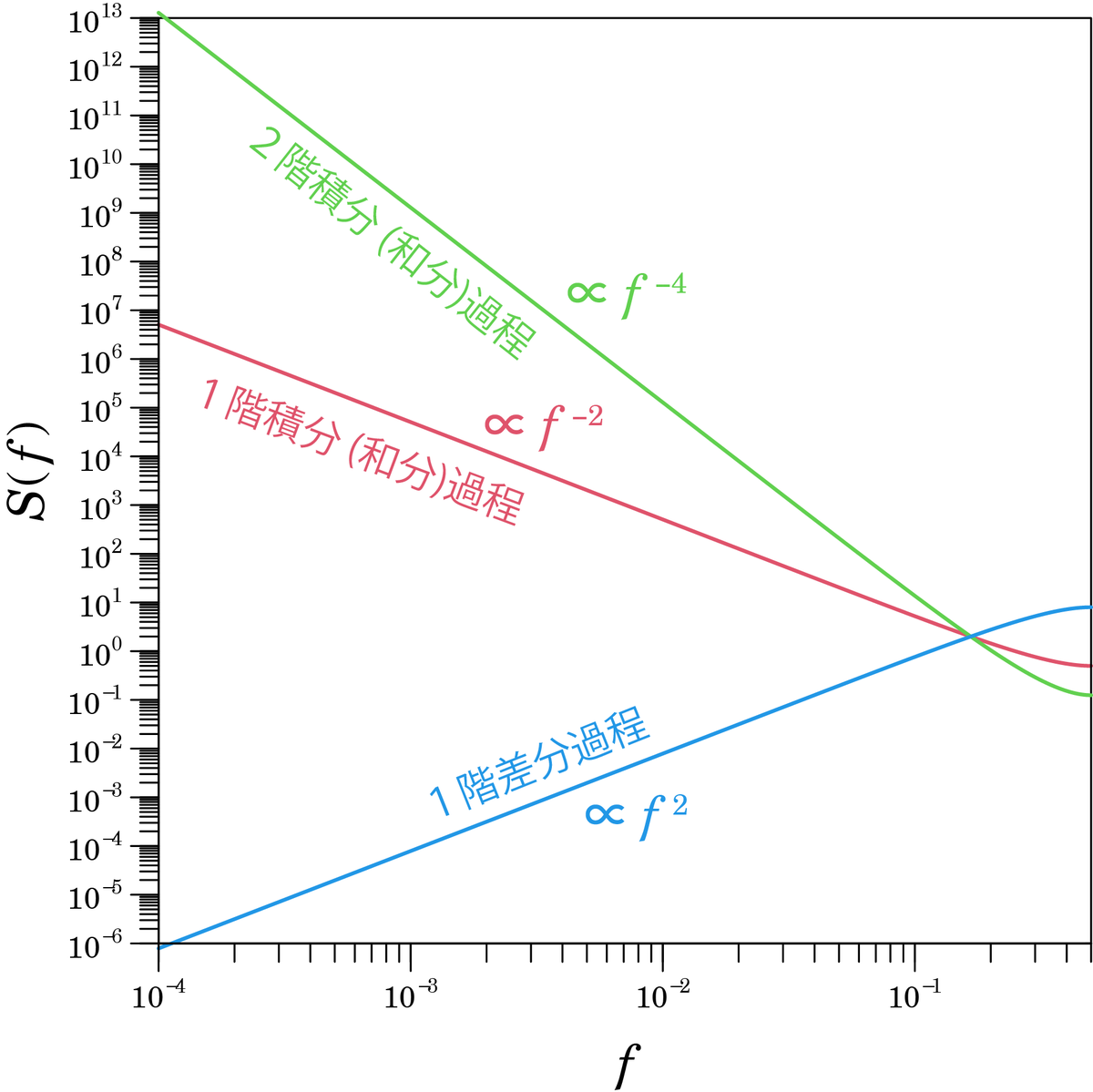
階積分 (和分)過程では,
,
階差分過程では,
になっています.解析的には,
についてマクローリン展開して,主要項だけ残せば,
あるいは,
となります.
ここから,のべき指数 (スケーリング指数)
を,連続的に変えるにはどうすればいいのか?と考えることで,今後,ARFIMA(0, d, 0)の話につなげます.