今回は,狭い意味での1/fゆらぎを生成します.ピンクノイズとも呼ばれます.なぜピンクかといえば,色とのアナロジーです.可視光の低周波数側の端が赤色なので,低周波側,つまり,白色よりも赤色が強調されていると考えられるので,色で言えば,どちらかといえば「ピンク」かなということです.
Rのパッケージで,非整数ガウスノイズのサンプル時系列を生成したり,非整数ブラウン運動のサンプル時系列を生成できたりしますが,その間にある狭い意味の「1/fゆらぎ」は生成できません.では,どうやれば,1/fゆらぎのサンプル時系列を生成できるでしょうか?ここでは,あくまで近似的に1/fゆらぎを生成します.
まず,1/fゆらぎを生成するためのパワースペクトルとして,
を仮定します (これ以外の方法もあります).は,非常に小さい定数です.この式のように
を含まず,
とすると,で発散していまいます.Rでの計算では,f=0で,Infが帰ってきます.それがいやなので,ここでは,
での
になるパワースペクトルを仮定します.完璧な1/fゆらぎは,パワースペクトルの面積が発散するということに注意してください.とはいえ,
を1/Nよりも十分小さくとれば,パワースペクトルの形状としては,ほぼ完璧な1/fゆらぎになります.(平均値を0に固定したければ,さらにS(f=0)=0としてください.)
パワースペクトルを仮定したあとは,白色ノイズを生成し,それを元に各周波数成分の振幅をパワースペクトルの平方根に従うように変えます.最後に,時系列の長さNで割って,逆フーリエ変換すれば,1/fゆらぎのサンプル時系列が得られます.平均と分散を設定したければ,その後に調整してください(以下では,設定してません).
ということで,Rスクリプトは以下です.時系列の長さNを設定すれば,と設定され,x.simに時系列が入ります.
# 時系列の長さ
N <- 1001
# 奇数に変換
N <- round(N/2)*2+1
# 半分
M <- (N-1)/2
#########################
# 1/fゆらぎの近似パワースペクトル
# f0は,高周波数側で無相関になるカットオフ周波数
PSD1.model <- function(f,f0){
return(1/(f0 + abs(f)))
}
#########################
# 両側パワースペクトル
f0 <- 1/(10*N)
f <- c((0:M)/N,-(M:1)/(N))
PSD.model <- PSD1.model(f,f0)
#########################
# 白色ノイズの生成
WN <- rnorm(N)
# ホワイトノイズのフーリエ変換
fft.WN <- fft(WN)
#########################
fft.sim <- sqrt(PSD.model)*fft.WN
#########################
x.sim <- Re(fft(fft.sim,inverse=TRUE))/Nきちんとできているか,検証するスクリプトが以下です.500個 (N.ensの値)のサンプルを生成して,平均のパワースペクトルと自己共分散関数を計算しています.
# 時系列の長さ
N <- 1001
# 奇数に変換
N <- round(N/2)*2+1
# 半分
M <- (N-1)/2
#########################
# 1/fゆらぎの近似パワースペクトル
# f0は,高周波数側で無相関になるカットオフ周波数
PSD1.model <- function(f,f0){
return(1/(f0 + abs(f)))
}
#########################
# 両側パワースペクトル
f0 <- 1/(10*N)
f <- c((0:M)/N,-(M:1)/(N))
PSD.model <- PSD1.model(f,f0)
##############################################
# サンプル時系列の総数
N.ens <- 500
PSD <- c()
ACOR <- c()
for(i in 1:N.ens){
#########################
# 白色ノイズの生成
WN <- rnorm(N)
# ホワイトノイズのフーリエ変換
fft.WN <- fft(WN)
#########################
fft.sim <- sqrt(PSD.model)*fft.WN
#########################
x.sim <- Re(fft(fft.sim,inverse=TRUE))/N
###############################################
# 以下は検証用プロット
################
TMP <- acf(x.sim,plot=FALSE,type="covariance",lag.max=round(N/10))
Ac.y <- TMP$acf[,,1]
X <- fft(x.sim)
S.y <- abs(X)^2/N
if(i == 1){
PSD <- S.y
ACOR <- Ac.y
}else{
PSD <- PSD+S.y
ACOR <- ACOR + Ac.y
}
}
PSD <- PSD/N.ens
ACOR <- ACOR/N.ens
################################################
# グラフ用パラメタ設定
par(mfrow=c(2,2),pty="m",cex=1.1)
plot(f[order(f)],PSD[order(f)],log="y",col=4,"l",lwd=2,xlim=c(-0.5,0.5),xaxs="i",xlab="f",ylab="PSD",main="Estimated Power Spectrum")
lines(f[order(f)],PSD.model[order(f)],col=2,lwd=2,lty=1)
legend("topright", legend=c("Model Power Spectrum"), col=c(2), lty=c(1),lwd=c(2))
plot(f[f>0],PSD[f>0],log="xy",col=4,"l",lwd=2,xlab="f",ylab="PSD",main="Estimated Power Spectrum")
lines(f[f>0],PSD.model[f>0],col=2,lwd=2,lty=1)
legend("topright", legend=c("Model Power Spectrum"), col=c(2), lty=c(1),lwd=c(2))
#
fit <- lm(log10(PSD[f>0])~log10(f[f>0]))
plot(log10(f[f>0]),log10(PSD[f>0]),col=4,pch=16,"l",lwd=2,xlab="f",ylab="PSD",main="Power Spectrum")
abline(fit,lty=2,col=2,lwd=2)
legend("topright", legend=c(paste("Fitted line with slope =",format(fit$coefficients[[2]],digit=2))), col=c(2), lty=c(2),lwd=c(2))
#################################################
k.lag <- 1:length(ACOR)-1
plot(k.lag[k.lag>0],ACOR[k.lag>0],pch=16,col=4,"o",log="x",lwd=2,xlim=c(1,N/10),xaxs="i",xlab="k",ylab="Autocovariance",main="Estimated Autocovariance")このスクリプトを実行すると以下のような図が出ると思います.
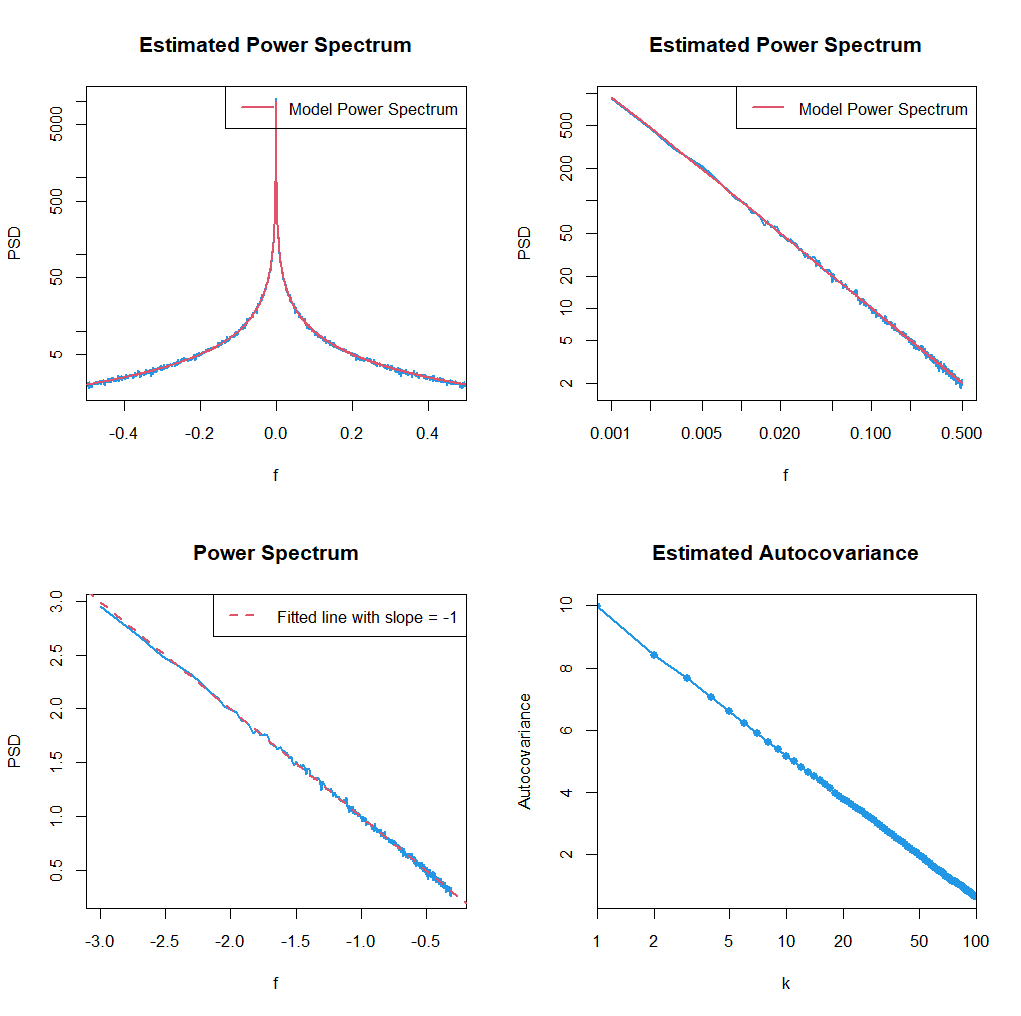
左下の図で,直線をフィットし,傾きを推定しています.右下の図は自己共分散関数の推定結果です.どのような関数になっているか分かりますか?興味がある人は,以下の論文を読んでみてください.
doi.org