【時系列解析】パワースペクトルの定義の確認 - ケィオスの時系列解析メモランダム

弱定常が仮定できる場合のパワースペクトルの定義について，まとめておきます．これまでの私の記事では，時系列のフーリエ変換から計算するものと，時系列の自己共分散関数（自己相関関数）から計算するものを，私のかってな都合にあわせて使い分けていました．全部同じものですので，ここでもう一度整理したいと思います（厳密さよりわかりやすさを優先します）．面倒なので，サンプリング間隔は1とします．

前提

弱定常ということは，確率過程のサンプル時系列が無限の長さになったとしても，

平均値が有限の値をとり，いつでも同じ

　（無限個のサンプル時系列を使って計算した各時刻の期待値がすべて同じ）

分散が有限の値をとり，いつでも同じ

　（無限個のサンプル時系列を使って計算した各時刻の分散がすべて同じ）

自己共分散（自己相関）関数が，2点間の時間差（ラグ）のみの関数で表される

を満たします．

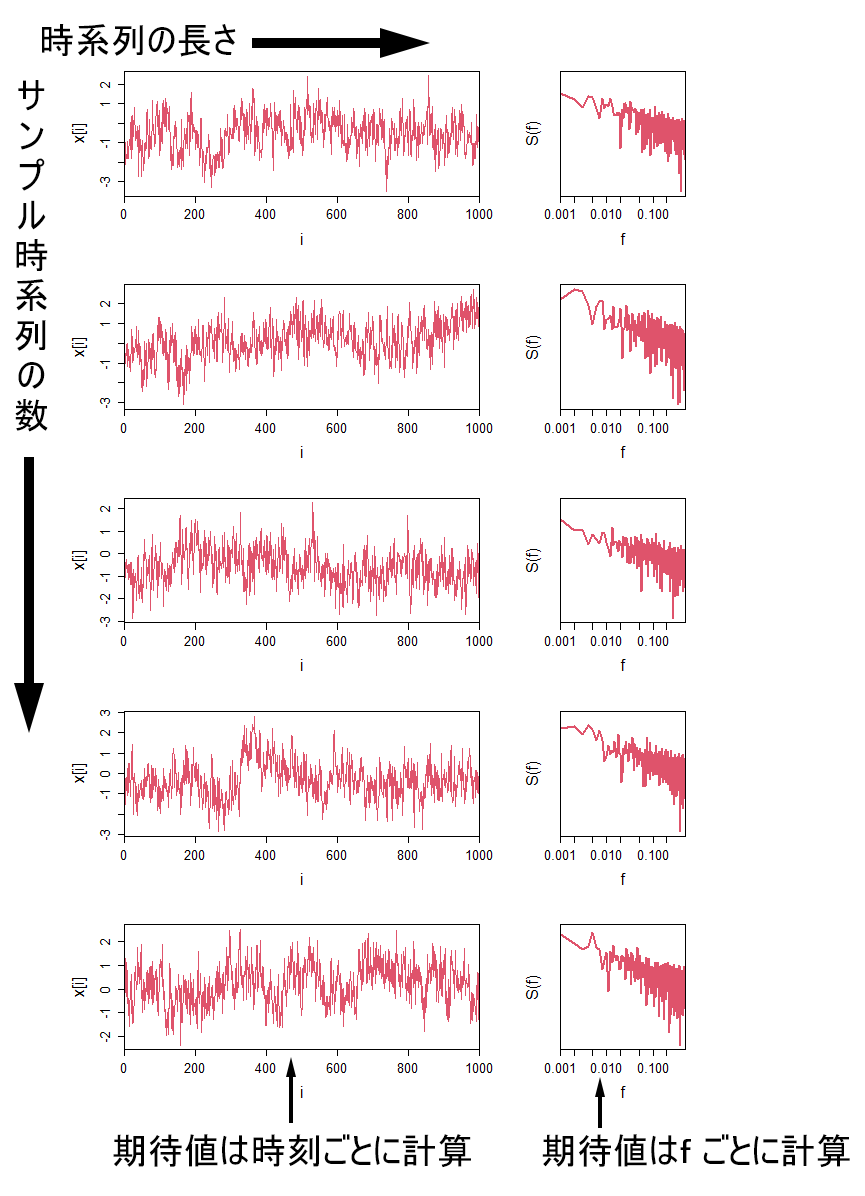
時間無限，サンプル数無限の説明のための図．左はサンプル時系列，右はそのパワースペクトルの推定量．

真のパワースペクトル

弱定常な確率過程で，無限の長さのサンプル時系列を，無限本発生させて，期待値をとったパワースペクトルが「真のパワースペクトル」です（上図参照）．実際の時系列解析では，有限の長さの時系列で，1本のサンプル時系列からパワースペクトルを計算すると思います．これは，真のパワースペクトルではなく，それを推定したものです．長さNの1本の時系列から計算したパワースペクトルの推定量を $\hat{S}_N (f)$ とすれば，真のパワースペクトルは，

　 $\displaystyle S (f) = {\rm E} \left[ \lim_{N \to \infty} \hat{S}_N (f) \right]$ 　
　（期待値は，たくさんの $\hat{S}_N (f)$ を使って， $f$ ごとに求めます）

です．

パワースペクトルの推定量

まずは，時系列を離散フーリエ変換するパターンです．長さNの時系列 $\{y [n]\}_{n=0}^{N-1}$ のパワースペクトルは，

　 $\displaystyle \hat{S}_N (f_k)= \frac{1 }{N} \left|\sum_{n=0}^{N-1} y [n] \, e^{- i 2 \pi f_k n} \right|^2$ 　 $\displaystyle \left(f_k = \frac{k}{N}\right)$

です．

つぎは，まず長さNの時系列の自己共分散（自己相関）関数の推定量 $\hat{C}[k]$ を計算し，その後に $\hat{C}[k]$ のフーリエ変換を計算するパターンです．このパターンは，使える条件があることに注意してください．
$\hat{C}[k]$ が， $|k|$ の増加にともない，そこそこ早く0に近づく場合のみ，パワースペクトルは，

　 $\displaystyle \hat{S}_N (f_k)= \sum_{n=-(N-1)}^{N-1} \hat{C}[n ] \, e^{- i 2 \pi f_k n} = \sum_{n=-(N-1)}^{N-1} \hat{C}[n ] \, \cos (2 \pi f_k n)$ 　 $\displaystyle \left(f_k = \frac{k}{N}\right)$