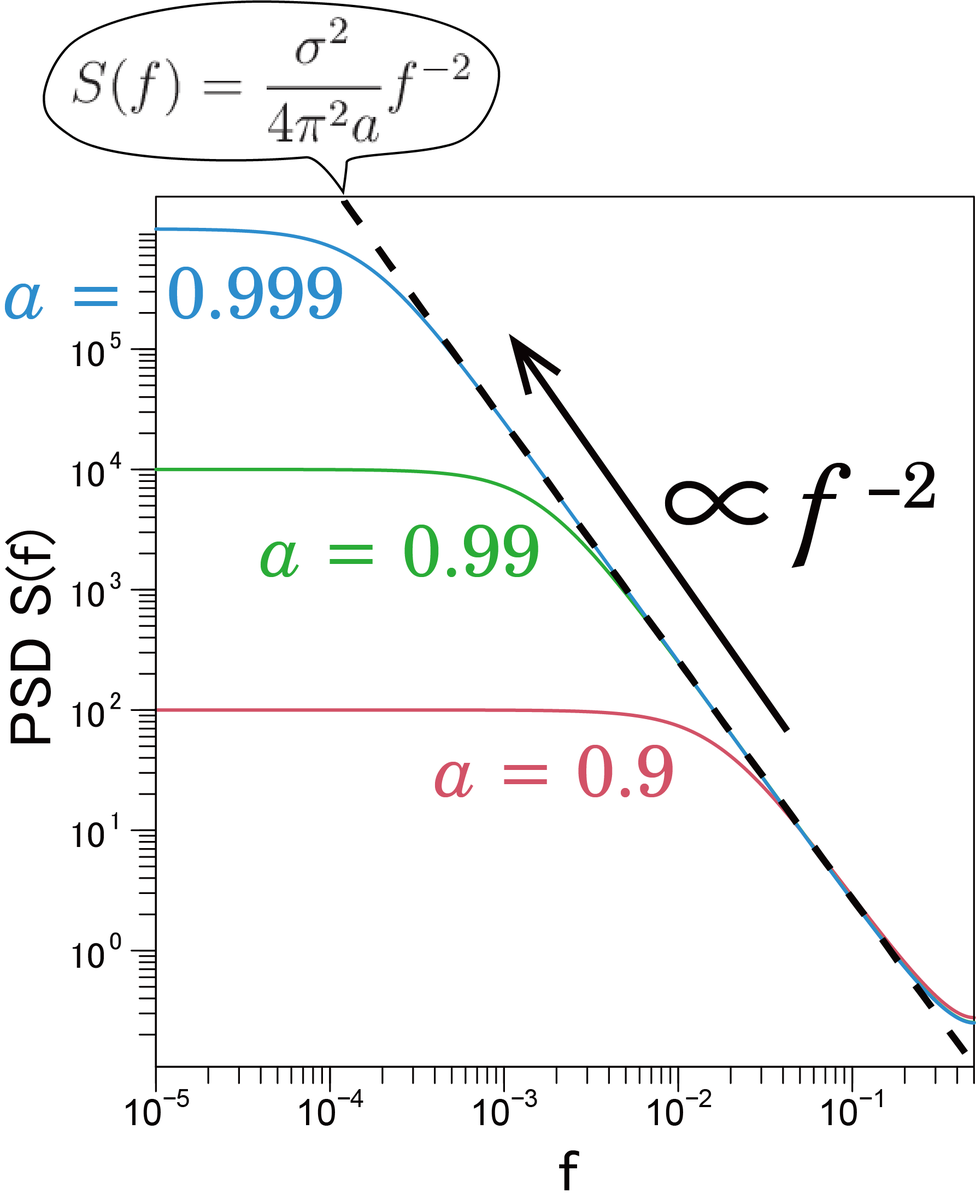
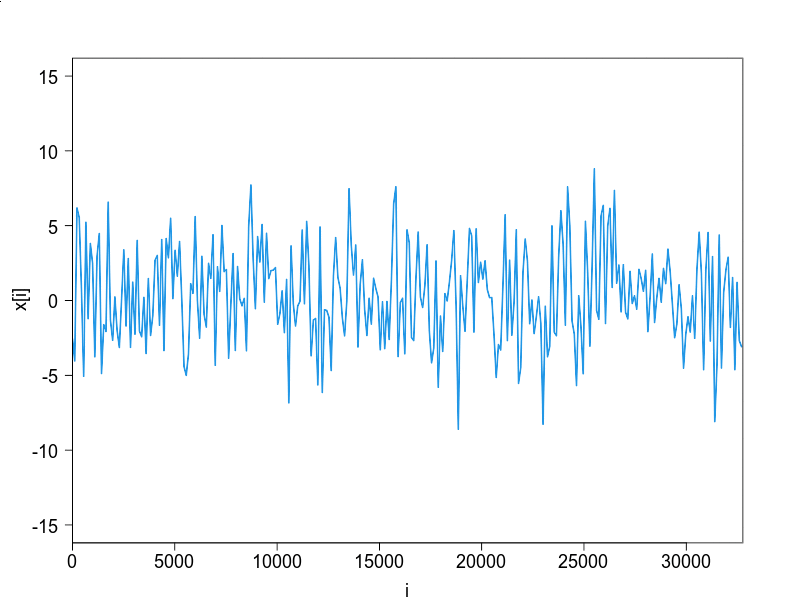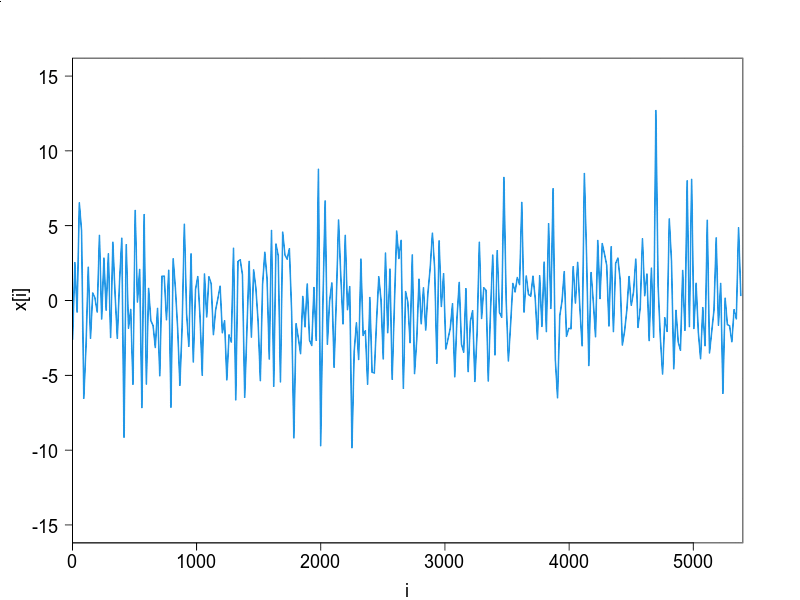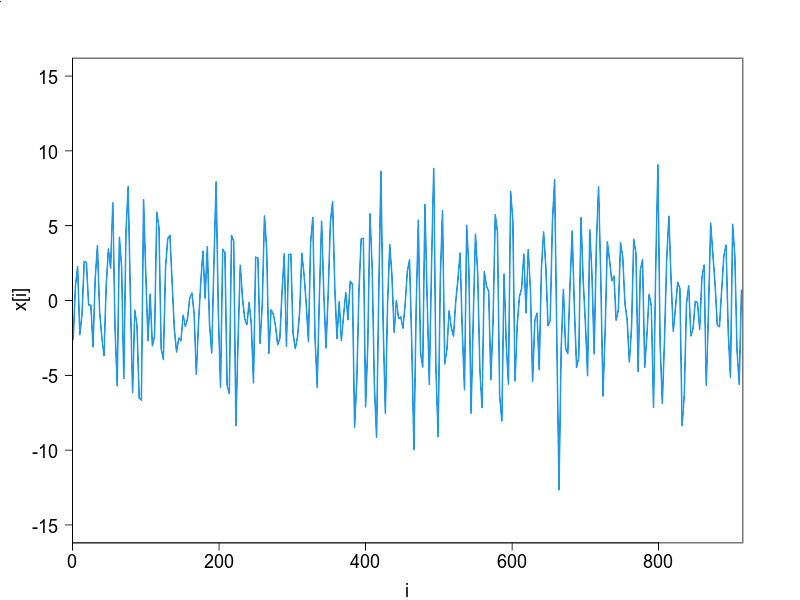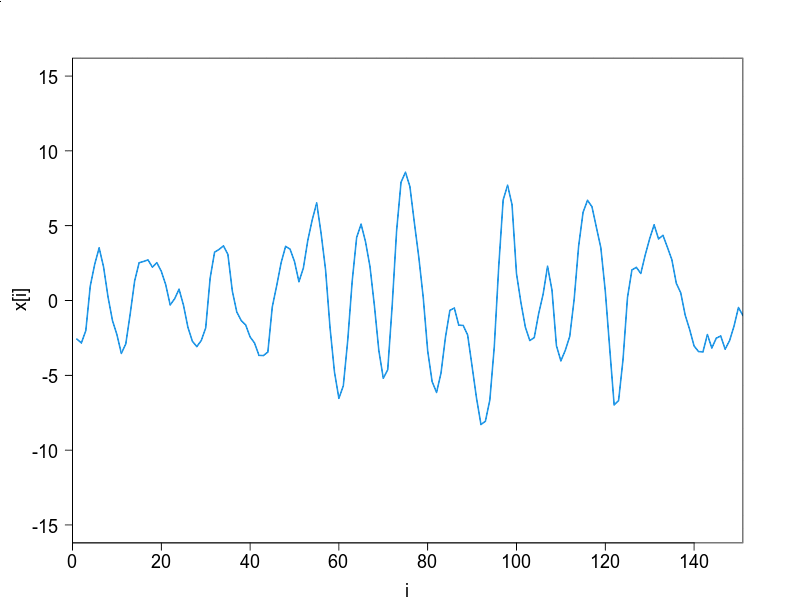
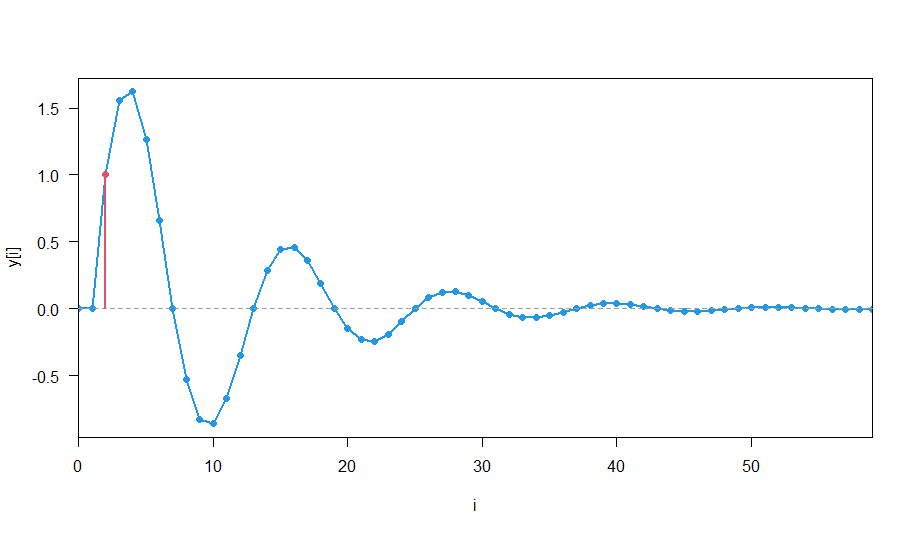
1次自己回帰過程は,短期記憶過程の典型例です.時系列解析の分野では,「記憶」とは「自己相関(自己共分散)」のことです.短期記憶過程では,特徴的な時間の長さがあり,その時間以上では記憶が消える,つまり,自己相関が0とみなせます.では,この自己相関が0とみなせる特徴的な時間の長さを,どのようにすれば見積もることができるのでしょうか.
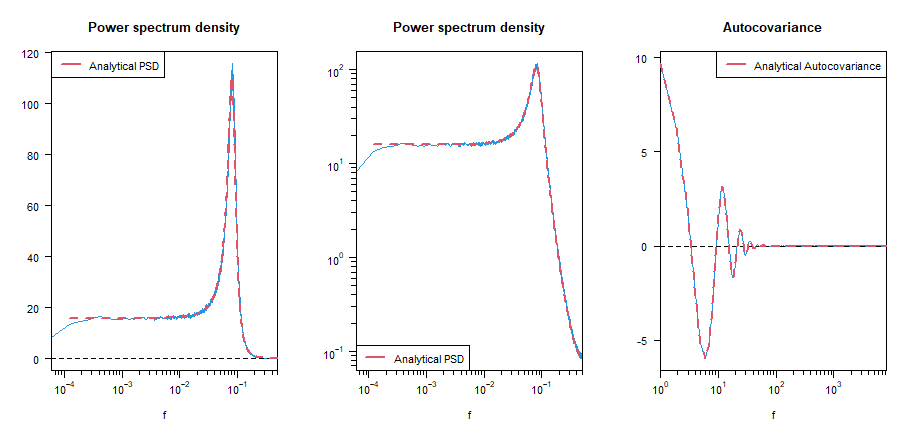
と近似できそうです.数学的な厳密さとか言われても私は数学者ではないので,数値的に検証します.検証した結果が下の図の右上です.水色の破線(近似)と赤の線(近似なし)が一致しているので,正しそうです.
おまけ
図の作成に使用したRスクリプト
a <- 0.98
par(mfrow=c(2,2))
par(pty="m",cex.axis=1.3,cex.lab=1.5,mar=c(5,5,2,2))
####################
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),log="xy",col=2,lwd=2,n=1000,xlim=c(0.00001,1/2),ylim=c(0.2,10000),xaxs="i",xlab="f",ylab="PSD S(f)",xaxt="n",yaxt="n")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
####################
curve(sig2/(1-2*a*cos(2*pi*x)+a^2),log="xy",col=2,lwd=2,n=1000,xlim=c(0.00001,1/2),ylim=c(0.2,10000),xaxs="i",xlab="f",ylab="PSD S(f)",xaxt="n",yaxt="n")
# 対数目盛を描く
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
axis(2,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(2,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
########################
abline(h=sig2/(1-a)^2,col=4,lwd=2,lty=2)
curve(sig2/(pi*x)^2/(4*a),add=TRUE,col=4,lwd=2,lty=2,xlim=c(0.00001,1/2))
#curve(sig2/(pi*x)^2/(4*a)*(pi*x)^2/sin(pi*x)^2,add=TRUE,col=5,lwd=2,lty=2,xlim=c(0.00001,1/2))
abline(v=(1-a)/(2*pi*sqrt(a)),col=4,lwd=2,lty=2)
#abline(v=-log(a)/(2*pi),col=1,lwd=2,lty=2)
####################################################
# 解析的に計算した自己共分散関数
curve(sig2/(1-a^2)*a^x,col=2,lwd=2,lty=1,xlim=c(1,10000),log="x",xaxs="i",xlab="k",ylab="Autocovariance C(k)",xaxt="n")
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
####################################################
# 解析的に計算した自己共分散関数
curve(sig2/(1-a^2)*a^x,col=2,lwd=2,lty=1,xlim=c(1,10000),log="x",xaxs="i",xlab="k",ylab="Autocovariance C(k)",xaxt="n")
axis(1,at=10^(-5:5)%x%(1:9),label=FALSE,tck=-0.02)
tmp<-paste(paste(sep="","expression(10^",-5:5,")"),collapse=",")
v.label<-paste("axis(1,las=1,at=10^(-5:5),label=c(",tmp,"),tck=-0.03)",sep="")
eval(parse(text=v.label))
abline(h=0,col=8,lwd=2,lty=2)
abline(v=-1/log(a),col=8,lwd=2,lty=2)
abline(v=-2*pi/log(a),col=4,lwd=2,lty=2)
とすれば,真のパワースペクトルは,
を使って,
ごとに求めます)
のパワースペクトルは,
を計算し,その後に
のフーリエ変換を計算するパターンです.このパターンは,使える条件があることに注意してください.
が,
の増加にともない,そこそこ早く0に近づく場合のみ,パワースペクトルは,
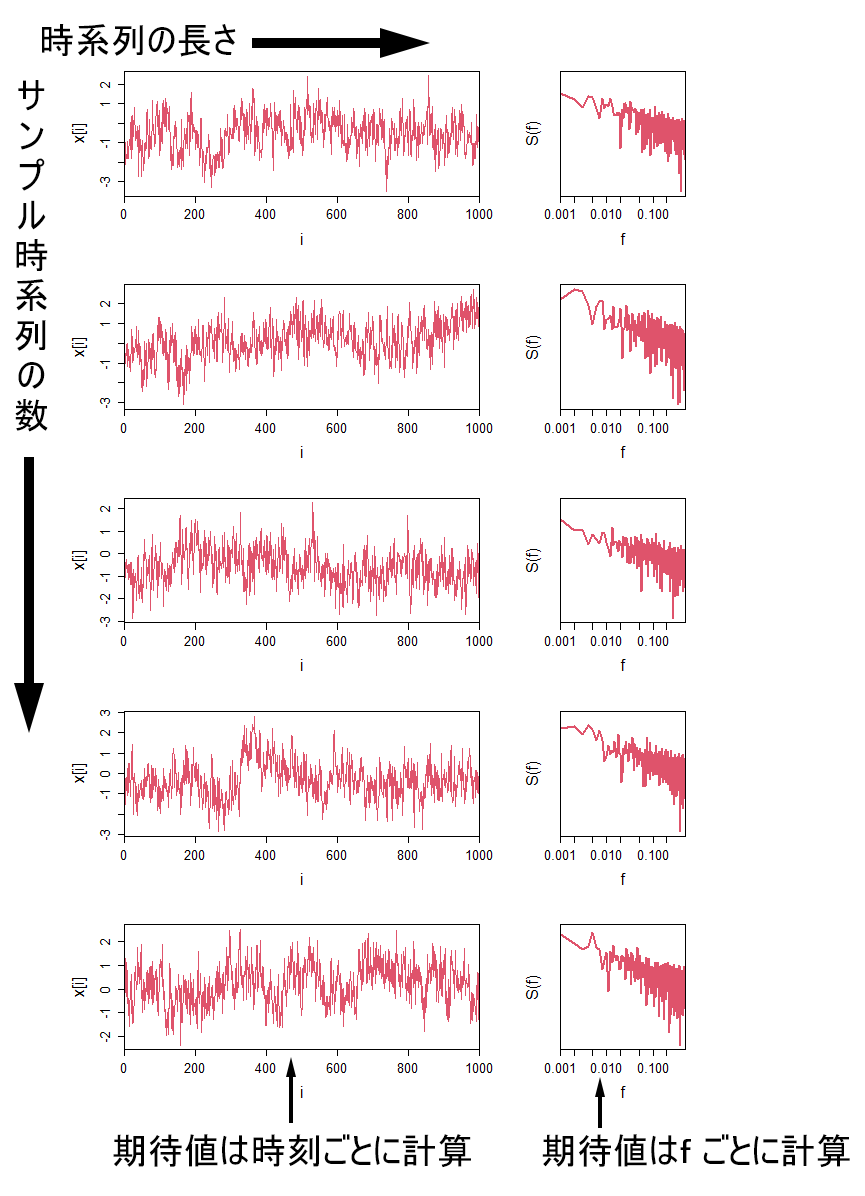
の推定量は,正定値性とが,何か小難しいことを言う場合の形です.
で割っても,たいした違いはありません.